Element RC

W obszarze elementów RC są rozumiane w elektrycznych obwodach rezystancyjnego rezystancji (R - Engl. Rezystor ) i kondensatora (C - Engl. Kondensatora ) są wykonane. Elementy RC są liniowymi, niezmiennymi w czasie układami . W węższym sensie odnosi się to do filtrów takich jak dolnoprzepustowy lub górnoprzepustowy . W przypadku dolnoprzepustowego, tak jak na sąsiednim rysunku, kondensator jest połączony równolegle na wyjściu sygnału, w przypadku górnoprzepustowego kondensator i rezystor są zamienione.

Kondensator i rezystor są połączone równolegle w celu wyrównania potencjałów i uziemienia funkcjonalnego . W celu ograniczenia zakłóceń elektromagnetycznych stosuje się szeregowe połączenia kondensatora i rezystora, jak np . tłumik .

Simple RC dolnoprzepustowy
U _e : napięcie wejściowe
U _a : napięcie wyjściowe

Zachowanie w dziedzinie czasu

Ogólny opis teoretyczno-systemowy filtra dolnoprzepustowego RC

Napięcia i prądy w dolnoprzepustowym RC

Element RC w konfiguracji dolnoprzepustowej jest integrującym, ciągłym w czasie, liniowym, niezmiennym w czasie elementem transmisyjnym. Ogólny opis teoretyczno-systemowy wynika z reguł Kirchhoffa i zależności prąd/napięcie na kondensatorze lub rezystorze. Równanie siatki daje

${\ displaystyle -u _ {\ tekst {e}} (t) + u _ {\ tekst {r}} (t) + u _ {\ tekst {c}} (t) = 0}$.

Ponieważ jest to obwód nierozgałęziony, obowiązują następujące zasady . Poniższe dotyczy spadku napięcia na rezystorze ${\ displaystyle ja _ {\ tekst {c}} (t) = ja _ {\ tekst {r}} (t)}$

${\ displaystyle u _ {\ tekst {r}} (t) = Ri _ {\ tekst {r}} (t)}$

A prąd płynący przez kondensator jest przez związek

${\ displaystyle i _ {\ tekst {c}} (t) = C {\ frac {{\ tekst {d}} u _ {\ tekst {c}} (t)} {{\ tekst {d}} t }} }$

zestaw. Jeśli teraz wstawimy równanie napięcia w poprzek rezystancji do równania siatki, otrzymamy

${\ displaystyle -u _ {\ tekst {e}} (t) + Ri _ {\ tekst {r}} (t) + u _ {\ tekst {c}} (t) = 0}$.

Wstawienie prądu ostatecznie daje równanie różniczkowe

${\ displaystyle RC {\ frac {{\ tekst {d}} u _ {\ tekst {c}} (t)} {{\ tekst {d}} t}} + u _ {\ tekst {c}} ( t) = u _ {\ tekst {e}} (t)}$,

który całkowicie opisuje element transmisyjny: Element RC ma proporcjonalne zachowanie transmisyjne z opóźnieniem pierwszego rzędu i odpowiada elementowi PT1 ze stałą czasową T = RC .

Aby wyjaśnić całkujący charakter filtra dolnoprzepustowego, przeprowadzimy jeszcze kilka przekształceń. Równanie jest zintegrowane po obu stronach

${\ displaystyle \ int RC {\ frac {{\ tekst {d}} u_ {c} (t)} {{\ tekst {d}} t}} \, {\ tekst {d}} t + \ int u_ { \ tekst {c}} (t) \, {\ tekst {d}} t = \ int u _ {\ tekst {e}} (t) \, {\ tekst {d}} t}$,

gdzie operatory różniczkowe i całkowe znoszą się nawzajem w wyrażeniu i następują

${\ displaystyle RCu _ {\ tekst {c}} (t) + \ int u _ {\ tekst {c}} (t) \, {\ tekst {d}} t = \ int u _ {\ tekst {e }} ( t) \, {\ tekst {d}} t}$.

Przełączanie zgodnie z napięciem wyjściowym ostatecznie skutkuje${\ styl wyświetlania u _ {\ tekst {c}} (t)}$

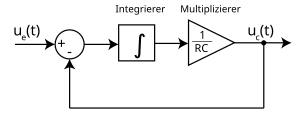
Schemat blokowy dolnoprzepustowego RC

${\ displaystyle u _ {\ tekst {c}} (t) = {\ frac {1} {RC}} \ lewo (\ int u _ {\ tekst {e}} (t) \, {\ tekst {d }} t- \ int u _ {\ tekst {c}} (t) \, {\ tekst {d}} t \ prawo) = {\ frac {1} {RC}} \ int \ lewo (u _ { \ tekst {e }} (t) \, - u _ {\ tekst {c}} (t) \ prawy) \, {\ tekst {d}} t}$.

Równanie całkowe w dziedzinie czasu można bezpośrednio poddać transformacji Laplace'a , która prowadzi do leads

${\ displaystyle u _ {\ tekst {c}} (s) = {\ frac {1} {RC}} {\ frac {1} {\ tekst {s}}} \ lewo (u _ {\ tekst {e }} (s) -u _ {\ tekst {c}} (s) \ prawo)}$

wyniki. Dzieląc sygnał wyjściowy przez sygnał wejściowy uzyskuje się funkcję przenoszenia dolnoprzepustowego RC: ${\ styl wyświetlania u _ {\ tekst {c}} (t)}$${\ styl wyświetlania u _ {\ tekst {e}} (t)}$

${\ displaystyle G _ {\ tekst {TP}} (s) = {\ frac {u _ {\ tekst {c}} (s)} {u _ {\ tekst {e}} (s)}} = { \ frac { 1} {1 + RC}}}$.

Ustalając (z jednostką urojoną i częstotliwością kątową ) transformację Fouriera, a tym samym reprezentację widmową systemu, otrzymujemy: ${\ styl wyświetlania s = \ matematyka {j} \ omega}$ ${\ styl wyświetlania \ matematyka {j}}$ ${\ styl wyświetlania \ omega}$

${\ displaystyle G _ {\ tekst {TP}} (\ matematyka {j} \ omega) = {\ frac {u _ {\ tekst {c}} (\ matematyka {j} \ omega)} {u _ {\ tekst {e }} (\ mathm {j} \ omega)}} = {\ frac {1} {1+ \ mathrm {j} \ omega RC}}}$.

Prawdopodobnie najważniejszą klasą sygnałów przy rozważaniu zachowania filtra są sygnały harmoniczne, dlatego często bardzo interesujące jest, jakie tłumienie ma filtr na sygnale sinusoidalnym. Przez sygnał wejściowy

Symulacja stanów nieustalonych z sinusoidalnym sygnałem wejściowym, R = 1 kΩ, C = 100 nF, f = 5 kHz

${\ displaystyle u _ {\ tekst {e}} (t) = {\ kapelusz {u}} \ grzech (\ omega t + \ varphi)}$

następnie następuje we wcześniej wyprowadzonym równaniu różniczkowym lub całkowym

${\ displaystyle RC {\ frac {{\ tekst {d}} u _ {\ tekst {c}} (t)} {{\ tekst {d}} t}} + u _ {\ tekst {c}} ( t) = u _ {\ tekst {e}} (t) = {\ kapelusz {u}} \ grzech (\ omega t + \ varphi)}$.

Aby znaleźć napięcie wyjściowe, musisz się przełączyć, jest to analitycznie możliwe. Jest to liniowe równanie różniczkowe zwyczajne, dla którego istnieje wiele różnych metod rozwiązywania. Jeśli weźmiemy pod uwagę warunek początkowy , czyli przypadek, w którym układ jest początkowo bez energii podczas osiadania, to rozwiązanie podaje wzór ${\ styl wyświetlania u _ {\ tekst {c}} (t)}$${\ styl wyświetlania u _ {\ tekst {c}} (0) = 0}$

${\ displaystyle u _ {\ tekst {c, sin}} (t) = {\ frac {{\ kapelusz {u}} \ po lewej (\ sin \ po lewej (\ omega t + \ varphi \ po prawej) -RC \ omega \ cos \ po lewej (\ omega t + \ varphi \ po prawej) \ po prawej) - {\ kapelusz {u}} {\ tekst {e}} ^ {- {\ frac {t} {RC}}} \ po lewej (\ sin (\ varphi) -RC \ omega \ cos (\ varphi) \ prawo)} {\ lewo (\ omega RC \ prawo) ^ {2} +1}}}$.

Ogólny opis teoretyczno-systemowy filtra górnoprzepustowego RC

Napięcia i prądy w górnoprzepustowym RC

Górnoprzepustowy RC jest również obwodem nierozgałęzionym, ale napięcie wyjściowe jest pobierane z rezystora. Z punktu widzenia teorii systemu jest różnicującym elementem transferu. Równanie siatki daje

${\ displaystyle -u _ {\ tekst {e}} (t) + u _ {\ tekst {r}} (t) + u _ {\ tekst {c}} (t) = 0}$.

Całkowity związek dotyczy napięcia na kondensatorze

${\ displaystyle u _ {\ tekst {c}} (t) = {\ frac {1} {C}} \ int i _ {\ tekst {c}} (t) \, {\ tekst {d}} t }$.

Ze względu na nierozgałęziony charakter obwodu następuje po wstawieniu ${\ displaystyle ja _ {\ tekst {c}} (t) = ja _ {\ tekst {r}} (t)}$

${\ displaystyle -u _ {\ tekst {e}} (t) + {\ frac {1} {C}} \ int i _ {\ tekst {r}} (t) \, {\ tekst {d}} t + u _ {\ tekst {r}} (t) = 0}$.

Prąd w całce można zapisać jako :, wstawiamy do równania: ${\ displaystyle ja _ {\ tekst {r}} (t) = {\ frac {u _ {\ tekst {r}} (t)} {R}}}$

${\ displaystyle -u _ {\ tekst {e}} (t) + {\ frac {1} {C}} \ int {\ frac {u _ {\ tekst {r}} (t)} {R}} \, {\ tekst {d}} t + u _ {\ tekst {r}} (t) = 0}$,

jest to równanie całkowe, które teraz w pełni opisuje układ. Aby zilustrować różniczkowy charakter filtra górnoprzepustowego, przeprowadzimy jeszcze kilka przekształceń. Równanie jest zróżnicowane po obu stronach

${\ displaystyle - {\ frac {\ tekst {d}} {{\ tekst {d}} t}} u _ {\ tekst {e}} (t) + {\ frac {1} {C}} {\ frac {\ tekst {d}} {{\ tekst {d}} t}} \ int {\ frac {u _ {\ tekst {r}} (t)} {R}} \, {\ tekst {d} } t + {\ frac {\ tekst {d}} {{\ tekst {d}} t}} u _ {\ tekst {r}} (t) = 0}$,

przy czym różniczka i operator całkowy znoszą się ponownie

${\ displaystyle - {\ frac {\ tekst {d}} {{\ tekst {d}} t}} u _ {\ tekst {e}} (t) + {\ frac {1} {RC}} u _ {\ tekst {r}} (t) + {\ frac {\ tekst {d}} {{\ tekst {d}} t}} u _ {\ tekst {r}} (t) = 0}$.

Przejście do rozmiaru początkowego skutkuje

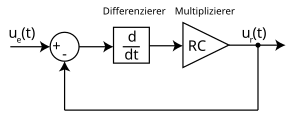
Schemat blokowy górnoprzepustowego RC.

${\ displaystyle u _ {\ tekst {r}} (t) = RC {\ frac {\ tekst {d}} {{\ tekst {d}} t}} \ lewo (u _ {\ tekst {e}} (t ) -u _ {\ tekst {r}} (t) \ prawo)}$,

dzięki czemu różnicujące zachowanie staje się oczywiste. Równanie można poddać transformacji Laplace'a , przy czym

${\ displaystyle u _ {\ tekst {r}} (s) = RCs \ lewo (u _ {\ tekst {e}} (s) -u _ {\ tekst {r}} (s) \ prawo)}$

następuje. Dzieląc sygnał wyjściowy przez sygnał wejściowy uzyskuje się funkcję przenoszenia górnoprzepustowego RC: ${\ styl wyświetlania u _ {\ tekst {r}} (t)}$${\ styl wyświetlania u _ {\ tekst {e}} (t)}$

${\ displaystyle G _ {\ tekst {HP}} (s) = {\ frac {u _ {\ tekst {r}} (s)} {u _ {\ tekst {e}} (s)}} = { \ frac { RCs} {1 + RCs}}}$

Ustawiając , uzyskuje się transformację Fouriera, a tym samym widmową reprezentację układu: ${\ styl wyświetlania s = \ matematyka {j} \ omega}$

${\ displaystyle G _ {\ tekst {HP}} (\ matematyka {j} \ omega) = {\ frac {u _ {\ tekst {r}} (\ matematyka {j} \ omega)} {u _ {\ tekst {e }} (\ mathrm {j} \ omega)}} = {\ frac {\ mathrm {j} \ omega RC} {1+ \ mathrm {j} \ omega RC}}}$.

Tutaj również rozważamy rozwiązanie równania różniczkowego dla harmonicznego sygnału wejściowego, dla którego można zastosować transformację Laplace'a. Sygnał wejściowy jest

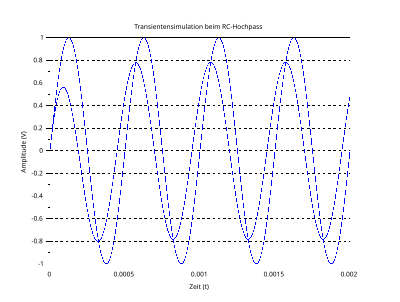
Symulacja stanów nieustalonych z sinusoidalnym sygnałem wejściowym, R = 1 kΩ, C = 100 nF, f = 2 kHz

${\ displaystyle u _ {\ tekst {e, sin}} (t) = {\ kapelusz {u}} \ grzech (\ omega t + \ varphi)}$,

którego przekształcenie Laplace'a jest

${\ displaystyle {\ mathcal {L}} \ lewo \ {{\ kapelusz {u}} \ grzech (\ omega t + \ varphi) \ prawo \} = {\ kapelusz {u}} {\ frac {\ omega \ cos (\ varphi) + s \ sin (\ varphi)} {s ^ {2} + \ omega ^ {2}}}}$.

Wstawienie do funkcji transferu zapewnia

${\ displaystyle u _ {\ tekst {r, grzech}} (s) = {\ frac {RCs} {1 + RCs}} {\ kapelusz {u}} {\ frac {\ omega \ cos (\ varphi) + s \ sin (\ varphi)} {s ^ {2} + \ omega ^ {2}}}}$.

Kompleksowa transformacja odwrotna prowadzi następnie do rozwiązania równania różniczkowego, a tym samym zachowania przejściowego dla sinusoidalnego sygnału wejściowego:

${\ displaystyle u _ {\ tekst {r, grzech}} (t) = {\ frac {{\ kapelusz {u}} {\ tekst {e}} ^ {- {\ frac {t} {RC}}} \ lewa (\ sin (\ varphi) - \ omega RC \ cos (\ varphi) \ prawa) + {\ hat {u}} \ omega RC \ lewa (\ cos (\ omega t + \ varphi) + \ omega RC \ sin (\ omega t + \ varphi) \ po prawej)} {\ po lewej (\ omega RC \ po prawej) ^ {2} +1}}}$

Proces ładowania

Jako przykład pokazano tutaj odpowiedź systemu na funkcję kroku . Napięcie wynosi zero woltów aż do punktu w czasie zero, a następnie natychmiast wzrasta . Prąd płynie do kondensatora, dopóki płytki nie zostaną naładowane elektrycznie i nie przyjmują żadnego dalszego ładowania. Dzieje się tak wtedy, gdy napięcie na kondensatorze U ( t ) równa jest przyłożone napięcie U _max jest. Jedna płytka jest wtedy elektrycznie dodatnia, druga ujemnie naładowana. Po stronie naładowanej ujemnie występuje nadmiar elektronów . ${\ styl wyświetlania U _ {\ rm {max}}}$

Czas ładowania kondensatora jest proporcjonalny do wielkości rezystora R i pojemności C kondensatora. Iloczyn rezystancji i pojemności nazywany jest stałą czasową .${\ styl wyświetlania \ tau}$

${\ styl wyświetlania \ tau = R \ cdot C \,}$

Teoretycznie trwa nieskończona ilość czasu, zanim U (t) = U _max . Dla celów praktycznych czas ładowania T _L może być stosowany, po czym kondensator mogą być traktowane jako w przybliżeniu do końca (ponad 99%) naładowany.

${\ displaystyle t_ {L} = 5 \ cdot \ tau \,}$

Krzywa napięcia U i prądu I podczas procesu ładowania,
U _max to napięcie źródła napięcia jako maksymalne możliwe napięcie

Stała czasowa τ oznacza również moment, w którym styczna przyłożona na początku krzywej osiąga końcową wartość napięcia. Po tym czasie kondensator byłby naładowany do swojej końcowej wartości, gdyby mógł być ładowany stałym prądem . W rzeczywistości jednak natężenie prądu zmniejsza się wykładniczo w czasie przy stałym przyłożonym napięciu. ${\ styl wyświetlania I _ {\ rm {max}}}$

Maksymalny prąd płynie w czasie t = 0. Wynika to z rezystancji R , zgodnie z prawem Ohma , gdzie U _{max jest} przyłożone napięcie źródła napięcia: ${\ styl wyświetlania I _ {\ rm {max}}}$

${\ displaystyle I _ {\ rm {max}} = {\ frac {U _ {\ rm {max}}} {R}} \,}$

Przebieg napięcia ładowania U ( t ) lub jego wartość w czasie opisuje się następującym równaniem, gdzie e to liczba Eulera , t to czas po rozpoczęciu ładowania i stała czasowa: ${\ styl wyświetlania \ tau}$

${\ displaystyle U (t) = U _ {\ rm {max}} \ cdot (1-e ^ {- {\ frac {t} {\ tau}}}) \,}$,

Zakłada się, że kondensator na początku nie był naładowany: . Dlatego po raz pierwszy napięcie wynosi zero, a następnie wzrasta w postaci funkcji wykładniczej . Po tym czasie napięcie osiągnie około 63% z zastosowanego napięcia U _max . Po tym czasie kondensator jest naładowany do ponad 99%. ${\ styl wyświetlania U (t = 0) = 0}$${\ styl wyświetlania t = \ tau}$${\ styl wyświetlania t = 5 \ tau}$

Przebieg natężenia prądu I ( t ) lub jego wartość w czasie opisuje równanie:

${\ displaystyle I (t) = ja _ {\ rm {max}} \ cdot e ^ {- {\ frac {t} {\ tau}}} \,}$

Tutaj prąd jest początkowo, a następnie maleje w postaci funkcji wykładniczej, jak w procesie rozładowania. Po tym czasie prąd wynosi tylko około 37% swojej wartości początkowej, a po tym czasie spadł do mniej niż 1%. ${\ styl wyświetlania I (t = 0) = ja _ {\ rm {max}}}$${\ styl wyświetlania t = \ tau}$${\ styl wyświetlania t = 5 \ tau}$

Równanie różniczkowe procesu ładowania

Poniższe informacje dotyczą procesu ładowania kondensatora dla idealnego źródła napięcia o napięciu : ${\ styl wyświetlania E}$

${\ displaystyle Q (t) = WE \ cdot \ lewo (1-e ^ {- {\ frac {t} {RC}}} \ po prawej)}$

Wynika to w następujący sposób. Poniższe informacje dotyczą natężenia prądu:

${\ displaystyle I (t) = {\ frac {\ matematyka {d} Q (t)} {\ matematyka {d} t}} = {\ kropka {Q}} (t)}$

Poniższe dotyczy napięcia na oporniku omowym:

${\ displaystyle U_ {R} = R \ cdot I (t) = R \ cdot {\ kropka {Q}} (t)}$

Poniższe dotyczy napięcia na kondensatorze:

${\ displaystyle U_ {C} = {\ frac {Q (t)} {C}}}$

W przypadku prostego obwodu składającego się z kondensatora i opornika omowego, zgodnie z zestawem siatek obowiązuje :

${\ displaystyle {\ begin {array} {crcl} & U_ {C} + U_ {R} & = & E \\\ Leftrightarrow & {\ Frac {Q (t)} {C}} + R \ cdot {\ kropka { Q}} (t) & = & E \\\ Leftrightarrow & {\ frac {1} {RC}} \ cdot Q (t) + {\ kropka {Q}} (t) & = & {\ frac {E} {R}} \\\ koniec {tablica}}}$

To równanie różniczkowe rozwiązuje się, najpierw rozwiązując równanie jednorodne przez pierwsze ustawienie: ${\ styl wyświetlania E / R = 0}$

${\ displaystyle \ int _ {t_ {0}} ^ {t} {\ frac {{\ kropka {Q}} (t)} {Q (t)}} \, \ mathm {d} t = \ int _ {t_ {0}} ^ {t} - {\ frac {1} {RC}} \, \ mathrm {d} t}$

Ponieważ jest stała, obowiązują następujące zasady: ${\ styl wyświetlania - {\ tfrac {1} {RC}}}$

${\ displaystyle \ int _ {t_ {0}} ^ {t} {\ frac {{\ kropka {Q}} (t)} {Q (t)}} \, \ matematyka {d} t = - {\ frac {1} {RC}} \ int _ {t_ {0}} ^ {t} 1 \, \ mathm {d} t}$

Zgodnie z zasadą substytucji :

${\ displaystyle \ ln \ lewy | Q (t) \ prawy | - \ ln \ lewy | Q (t_ {0}) \ prawy | = - {\ frac {t-t_ {0}} {RC}}}$

${\ styl wyświetlania Q_ {v}}$jest oczekiwaną nazwą metody użytej w kolejnych krokach zmiana stałych , czy ładunek elektryczny kondensatora w danym momencie , nie może stać się ujemny , czy jest punktem w czasie na początku ładowania i ma wartość 0 s; wynika: ${\ styl wyświetlania Q (t)}$${\ styl wyświetlania t}$${\ styl wyświetlania t_ {0}}$

${\ displaystyle \ ln \ lewo ({\ frac {Q (t)} {Q_ {v}}} \ prawo) = - {\ frac {t} {RC}}}$

Podniesienie podstawy e do potęgi daje:

${\ displaystyle {\ frac {Q (t)} {Q_ {v}}} = e ^ {- {\ frac {t} {RC}}} \ lewoprawa strzałka Q (t) = Q_ {v} \ cdot e ^ {- {\ frac {t} {RC}}}}$

Aby móc teraz rozwiązać niejednorodne równanie różniczkowe, stosujemy metodę różnicowania stałych , uznając je za zależne od czasu i wstawiając je takie, jakie są i zróżnicowanie do równania wyjściowego. ${\ displaystyle Q_ {v} (t)}$

${\ displaystyle {\ kropka {Q}} (t) = {\ kropka {Q}} _ {v} (t) \ cdot e ^ {- {\ frac {t} {RC}}} - {\ frac { Q_ {v} (t)} {ŻW}} \ cdot e ^ {- {\ frac {t} {ŻW}}}}$

używać w:

${\ displaystyle {\ zacząć {tablica} {rcl} {\ frac {E} {R}} & = & {\ frac {1} {RC}} \ cdot Q (t) + {\ kropka {Q}} ( t) \\ & = & {\ frac {Q_ {v} (t)} {ŻW}} \ cdot e ^ {- {\ frac {t} {ŻW}}} + {\ kropka {Q}} _ { v} (t) \ cdot e ^ {- {\ frac {t} {ŻW}}} - {\ frac {Q_ {v} (t)} {ŻW}} \ cdot e ^ {- {\ frac {t } {PC}}} \\ & = & {\ kropka {Q}} _ {v} (t) \ cdot e ^ {- {\ frac {t} {RC}}} \\\ end {tablica}} }$

Zostanie to przekształcone i zintegrowane zgodnie z: ${\ styl wyświetlania {\ kropka {Q}} _ {v} (t)}$

${\ displaystyle {\ begin {tablica} {rcl} \ int _ {t_ {0}} ^ {t} {\ kropka {Q}} _ {v} (t) \, \ mathrm {d} t & = & \ int _ {t_ {0}} ^ {t} {\ frac {E} {R}} \ cdot e ^ {\ frac {t} {RC}} \, \ mathrm {d} t \\ Q_ {v } (t) -Q_ {v} (t_ {0}) & = & {\ frac {E} {R}} \ cdot RC \ lewo (e ^ {\ frac {t} {RC}} - e ^ { \ frac {t_ {0}} {RC}} \ po prawej) \ end {tablica}}}$

Jak wspomniano powyżej, ładowanie rozpoczyna się w momencie . W tym momencie ładunek na kondensatorze wynosi : ${\ styl wyświetlania t_ {0} = 0}$${\ displaystyle Q_ {v} (t_ {0}) = 0}$

${\ displaystyle {\ zacząć {tablica} {rcl} Q_ {v} (t) -0 & = & EC \ lewo (e ^ {\ frac {t} {RC}} - e ^ {\ frac {0} { RC} } \ prawo) \\ Q_ {v} (t) & = & EC \ cdot \ lewo (e ^ {\ frac {t} {RC}} - 1 \ prawo) \\\ end {tablica}}}$

To musi być wprowadzone do rozwiązania DGL:

${\ displaystyle {\ początek {tablica} {rcl} Q (t) & = & Q_ {v} \ cdot e ^ {- {\ frac {t} {RC}}} \\ & = & EC \ cdot \ lewo (e ^ {\ frac {t} {RC}} - 1 \ po prawej) \ cdot e ^ {- {\ frac {t} {RC}}} \\ & = & EC \ cdot \ po lewej (1-e ^ {- { \ frac {t} {RC}}} \ po prawej) \ koniec {tablica}}}$

To jest równanie jak powyżej. Jeśli jako wartość wybierzesz teoretycznie w pełni naładowany kondensator, równanie to: ${\ Displaystyle EC = Q_ {E}}$

${\ displaystyle Q (t) = Q_ {E} \ cdot \ po lewej (1-e ^ {- {\ frac {t} {RC}}} \ po prawej)}$

To samo dotyczy napięcia : ${\ styl wyświetlania U}$

${\ displaystyle U (t) = {\ frac {Q (t)} {C}} = E \ cdot \ po lewej (1-e ^ {- {\ frac {t} {RC}}} \ po prawej)}$

a dla natężenia : ${\ styl wyświetlania I (t)}$

${\ displaystyle I (t) = {\ kropka {Q}} (t) = \ lewo ({\ frac {WE} {RC}} \ prawo) \ cdot e ^ {- {\ frac {t} {RC} }} = I_ {0} \ cdot e ^ {- {\ frac {t} {RC}}}}$

Proces rozładunku

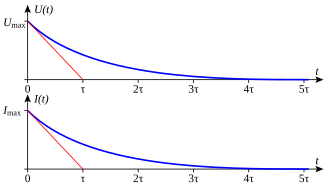
Krzywa napięcia U i prądu I podczas procesu rozładowania,
U _max jest napięciem początkowym

Rysunek przedstawia proces rozładowania, gdy kondensator jest wstępnie naładowany do wartości U _max i jest odprowadzane przez rezystor R. Zarówno napięcie, jak i prąd są tu na początku największe:

Dla t = 0 obowiązuje następująca zasada:    i jest w dowolnym momencie po tym czasie    ${\ displaystyle I _ {\ rm {max}} = {\ frac {U _ {\ rm {max}}} {R}}}$${\ Displaystyle I (t) = {\ Frac {U (t)} {R}}}$

Napięcie spada z czasem zgodnie z przebiegiem rozładowania

${\ displaystyle U (t) = U _ {\ rm {max}} \ cdot e ^ {- {\ frac {t} {\ tau}}} \,}$

Prąd, który jest połączony z napięciem U (t) przez rezystor rozładowujący R, pokazuje odpowiednią krzywą

${\ displaystyle I (t) = ja _ {\ rm {max}} \ cdot e ^ {- {\ frac {t} {\ tau}}} \,}$

Prąd rozładowania jest ujemny w określonym kierunku strzałki zliczania.

Równanie różniczkowe wyładowania

Następujące zasady dotyczą procesu rozładowywania kondensatora:

${\ displaystyle Q (t) = Q_ {0} \ cdot e ^ {- {\ frac {t} {RC}}}}$

Wynika to jak w procesie ładowania. Stąd można pobrać rozwiązane równanie różniczkowe. Warunki początkowe są po prostu inne i metoda zmieniania stałych nie jest wymagana:

${\ displaystyle \ ln \ lewy | Q (t) \ prawy | - \ ln \ lewy | Q (t_ {0}) \ prawy | = - {\ frac {t-t_ {0}} {RC}}}$

${\ styl wyświetlania Q (t)}$jest ładunkiem elektrycznym kondensatora w danym momencie , nie może stać się ujemnym, jest punktem w czasie na początku rozładowania i ma wartość 0 s. Nie ma tutaj rozładowania, ale ładunek początkowy ; wynika: ${\ styl wyświetlania t}$${\ styl wyświetlania t_ {0}}$${\ styl wyświetlania Q_ {0}}$

${\ displaystyle \ ln \ lewo ({\ frac {Q (t)} {Q (0)}} \ prawo) = - {\ frac {t} {RC}}}$

Podniesienie podstawy e do potęgi daje:

${\ displaystyle {\ frac {Q (t)} {Q_ {0}}} = e ^ {- {\ frac {t} {RC}}} \ Strzałka w lewo w prawo Q (t) = Q_ {0} \ cdot e ^ {- {\ frac {t} {RC}}}}$

To samo dotyczy napięcia : ${\ styl wyświetlania U}$

${\ displaystyle U (t) = {\ frac {Q (t)} {C}} = U_ {0} \ cdot e ^ {- {\ frac {t} {RC}}}}$

a dla natężenia : ${\ styl wyświetlania I}$

${\ displaystyle I (t) = {\ kropka {Q}} (t) = - I_ {0} \ cdot e ^ {- {\ frac {t} {RC}}}}$

Odpowiedź impulsowa

Przebieg prądu ładowania (niebieski) i napięcia kondensatora (różowy) na elemencie RC na impulsie napięciowym

Odpowiedź impulsowa opisuje krzywą napięcia wyjściowego przy bezpośrednim impulsowym napięciu wejściowym. Krzywą napięcia wyjściowego opisuje jego pochodna w czasie:

${\ displaystyle {\ kropka {U}} (t) = {\ frac {dU} {dt}} = {\ frac {U_ {q}} {\ tau}} e ^ {- {\ frac {t} { \ tau}}} \,}$

Jest to chwilowe napięcie na rezystorze, które powoduje odwrócenie ładowania kondensatora. Impuls napięciowy jest integrowany przez element RC i pozostawia ładunek kondensatora, który jest następnie rozładowywany w postaci funkcji wykładniczej. ${\ styl wyświetlania {U_ {q}}}$

Szybkość wzrostu napięcia (wolty na sekundę) jest ważną zmienną w elektronice i energoelektronice. ${\ displaystyle {\ frac {dU} {dt}}}$

Sygnały okresowe

Krzywa czasowa napięcia (niebieski) na kondensatorze, który jest okresowo ładowany i rozładowywany przez rezystor z idealnego prostokątnego źródła napięcia (czerwony)

Efekt filtra jest szczególnie wyraźny w przypadku sygnałów o przebiegu prostokątnym; odpowiedź filtra składa się z segmentów zachowania ładowania i rozładowania. Nachylenie staje się mniejsza, a zatem wysokich częstotliwości brak w widmie częstotliwości. Elementy RC są stosowane odpowiednio do tłumienia zakłóceń oraz jako filtr dolnoprzepustowy .

Nachylenie krawędzi napięcia na kondensatorze w amplitudzie U ₀ źródło napięcia prostokątny spada z nieskończonej wartości napięcia prostokątnego podawania do maksimum

${\ displaystyle {\ frac {dU} {dt}} = {\ frac {U_ {0}} {RC}} = {\ frac {U_ {0}} {\ tau}}}$.

z. Maksymalny prąd ładowania (prąd szczytowy, prąd impulsowy I _p ) wynosi

${\ displaystyle {I_ {p}} = {\ frac {U_ {0}} {R}}}$.

Na przykład styki przełączające lub przełączniki półprzewodnikowe podłączone do tłumika RC muszą być w stanie wytrzymać ten prąd .

Zachowanie w domenie częstotliwości

Dolnoprzepustowy

Odpowiedź amplitudowa filtra dolnoprzepustowego RC. Na rzędnej przedstawia stosunek amplitudy w decybelach The odcięta znormalizowanej częstotliwości kątowej Ohm w logarytmicznej reprezentacji .${\ styl wyświetlania | H |}$

Przesunięcie fazowe w funkcji znormalizowanej częstotliwości Ω na elemencie RC.

Przesunięcie fazowe o 90 ° między prądem a napięciem na kondensatorze

Z, R, Xc

V, Vr, Vc

Rezystor i kondensator tworzą dzielnik napięcia zależny od częstotliwości , co również powoduje przesunięcie fazowe maksymalnie (90°). W impedancji Z mają R i . Poniższe dotyczy elementu RC dla harmonicznego napięcia oscylacyjnego o częstotliwości : ${\ displaystyle {\ frac {\ pi} {2}}}$ ${\ styl wyświetlania 1 / (\ matematyka {j} \ omega C)}$ ${\ displaystyle f = {\ frac {\ omega} {2 \ pi}}}$

${\ displaystyle U_ {a} = U_ {e} \ cdot {\ frac {Z_ {C}} {Z_ {R} + Z_ {C}}} \,}$

a tym samym dla zachowania transmisji , które definiuje się jako iloraz napięcia wyjściowego do napięcia wejściowego:

${\ displaystyle H = {\ frac {U_ {a}} {U_ {e}}} = {\ frac {Z_ {C}} {Z_ {R} + Z_ {C}}} = {\ frac {\ frac {1} {\ mathrm {j} \ omega C}} {R + {\ frac {1} {\ mathrm {j} \ omega C}}}} = {\ frac {1} {1+ \ mathrm {j } \ omega RC}} = {\ frac {1} {1+ \ mathrm {j} {\ mathit {\ Omega}}}} \,}$,

gdzie znormalizowana częstotliwość Ω = ω / ω ₀ wynika z dzielenia częstotliwości kątowej ω = 2π f i granicznej częstotliwości kątowej (częstotliwość przejścia, częstotliwość graniczna ) ω _c = 1 / τ = 1 / ( RC ). Daje to częstotliwość odcięcia f _c , przy której reaktancja i rezystancja przyjmują tę samą wartość, czyli przesunięcie fazowe (45°) i tłumienie wynosi około 3 dB: ${\ displaystyle {\ frac {\ pi} {4}}}$

${\ displaystyle f_ {c} = {\ frac {1} {2 \ pi \ cdot R \ cdot C}} \,}$

Dla niskich częstotliwości Ω  << 1, H wynosi około 1, napięcie wejściowe i wyjściowe mniej więcej takie same, dlatego nazywa się również zakres. określany jako pasmo przepustki .
Dla częstotliwości Ω  >> 1, H spada o 20 dB na dekadę = 6 dB na oktawę. Odfiltrowany obszar nazywany jest pasmem zatrzymania .

Przy bardzo niskich częstotliwościach, które są znacznie niższe od częstotliwości odcięcia, prąd ładowania kondensatora nie ma znaczenia, a napięcie wejściowe i wyjściowe różnią się tylko niezauważalnie. Przesunięcie fazowe wynosi około 0 °.

Jeśli częstotliwość wzrasta, trwa to coraz dłużej – w porównaniu z okresem oscylacji – zanim kondensator zostanie naładowany do napięcia wejściowego. Dlatego przesunięcie fazowe wzrasta.

Przy bardzo wysokiej częstotliwości dąży to do wartości granicznej 90 °, ale wtedy napięcie na kondensatorze jest również niezmiernie małe.

Wysokoprzepustowy

Połączenie filtra górnoprzepustowego różni się od połączenia filtra dolnoprzepustowego zamianą R i C . Odpowiednio,

${\ displaystyle U_ {a} = U_ {e} \ cdot {\ frac {Z_ {R}} {Z_ {C} + Z_ {R}}} \,}$

i

${\ displaystyle H = {\ frac {U_ {a}} {U_ {e}}} = {\ frac {Z_ {R}} {Z_ {C} + Z_ {R}}} = {\ frac {R} {{\ ułamek {1} {\ ułamek {j} \ omega C}} + R}} = {\ ułamek {\ ułamek {j} \ omega R} {1+ \ macierz {j} \ omega R}} = {\ Frac {\ mathrm {j} {\ mathit {\ Omega}}} {1+ \ mathrm {j} {\ mathit {\ Omega}}}} \,}$,

Odpowiedź amplitudy jest  odzwierciedlona w stosunku do dolnego pasma wzdłuż Ω = 1, wysokie częstotliwości mogą przechodzić prawie bez tłumienia.

Opis w zakresie spektralnym

Z wyprowadzeniem analogowym otrzymujemy dla dolnoprzepustowego

${\ Displaystyle H (s) = {\ Frac {1} {1 + sRC}} \,}$,

słup w . ${\ styl wyświetlania s = -1 / RC}$

Na wysokiej przełęczy

${\ displaystyle H (s) = {\ frac {sRC} {1 + sRC}} \,}$,

jest też biegun w , plus zero w początku. Element RC reprezentuje zatem filtr Butterwortha pierwszego rzędu. ${\ styl wyświetlania s = -1 / RC}$

linki internetowe

• Interaktywne wyświetlanie procesu ładowania i rozładowywania w czasie. W: GeoGebra . Źródło 5 stycznia 2021 
• Obliczanie elementów RC częstotliwości przejścia i stałej czasowej
• Animacja ładowania i rozładowywania kondensatora