Moc (matematyka)

Notacja potęgi: ${\ displaystyle {\ tekst {wartość potęgi}} = {\ tekst {podstawa}} ^ {\ tekst {wykładnik}}}$

Moc (od Łacińskiej potentia „zdolności, mocy” ) jest wynikiem podnoszenia do potęgi ( potęgowanie ), który, podobnie jak mnożenie jest skrócona notacja dla powtarzanych matematycznych operacji arytmetycznych . Podobnie jak do składnika jest wielokrotnie dodane podczas mnożenia , czynnikiem jest wielokrotnie pomnożyć kiedy exponentiating . Liczba do pomnożenia nazywana jest podstawą. Jak często ta podstawa występuje jako czynnik, wskazuje wykładnik . Pisze się:

${\ displaystyle {\ tekst {wartość potęgi}} = {\ tekst {podstawa}} ^ {\ tekst {wykładnik}}}$

definicja

Mówi się jak a do potęgi n , n -tej potęgi a , a do n-tej potęgi lub w skrócie a do n-tej . W tym przypadku , a (do) plac jest także powszechne. ${\ displaystyle a ^ {n}}$${\ styl wyświetlania n = 2}$

${\ styl wyświetlania a}$nazywana jest podstawą (lub liczbą podstawową ), nazywana jest wykładnikiem (lub wykładnikiem ) potęgi . Wynik jest nazywany mocą lub wartością mocy.${\ styl wyświetlania n}$ ${\ displaystyle a ^ {n}}$

W definicji zbiorów zarówno po stronie wykładnik i od strony podstawy są rozszerzone krok po kroku, w dalszej części.

Wykładniki naturalne

Potencja dotyczy liczb rzeczywistych lub zespolonych (elementy wspólne dowolnego monoidu multiplikatywnego ) i liczb naturalnych przez ${\ displaystyle a ^ {n}}$${\ styl wyświetlania a}$${\ styl wyświetlania n}$

${\ displaystyle {\ początek {macierz} a ^ {n}: = \ pod nawiasem {a \ cdot a \ cdot a \ dotsm a} _ {n \ \ mathrm {czynniki}} \ koniec {macierz}}}$

Są określone. Ta definicja dotyczy tylko Tak, że tożsamość, która z niej wynika (również tylko dla ) dotyczy również , jest określona. ( Zobacz poniżej komentarze do sprawy .) ${\ styl wyświetlania n = 1,2,3, \ kropki}$${\ styl wyświetlania n = 1,2,3, \ kropki}$ ${\ displaystyle a \ cdot a ^ {n} = a ^ {n + 1}}$${\ styl wyświetlania n = 0}$${\ displaystyle a ^ {0}: = 1}$${\ styl wyświetlania a = 0}$

Funkcje potęgowe z dodatnimi wykładnikami graficznie

Funkcje potęgowe z ujemnymi wykładnikami graficznie

Poniższa modyfikacja ułatwia obsługę szczególnego przypadku : ${\ styl wyświetlania n = 0}$

Notacja potęgowa oznacza „mnożenie liczby 1 przez liczbę podstawową tak często, jak wskazuje wykładnik”, tj

${\ displaystyle {\ begin {macierz} a ^ {n} = 1 \ cdot \ underbrace {a \ cdot a \ cdot a \ dotsm a} _ {n \ \ mathrm {czynniki}}. \ end {macierz}}}$

Wykładnik 0 mówi, że liczba 1 nigdy nie jest mnożona przez liczbę podstawową i pozostaje sama, więc wynikiem jest 1.

${\ displaystyle {\ początek {wyrównany} a ^ {2} & = 1 \ razy a \ razy a \\ a ^ {1} & = 1 \ razy a \\ a ^ {0} & = 1 \ koniec {wyrównany }}}$

Przy ujemnej podstawie i parzystym wykładniku potęga jest dodatnia:

${\ displaystyle (- | a |) ^ {2n} = | a | ^ {2n}}$

Przy ujemnej podstawie i nieparzystym wykładniku potęga jest ujemna:

${\ displaystyle (- | a |) ^ {2n + 1} = - | a | ^ {2n + 1}}$

Całe ujemne wykładniki

Ujemne wykładniki oznaczają, że należy wykonać operację ( dzielenie ) odwrotną do mnożenia . Tak więc „Podziel liczbę 1 przez liczbę podstawową tak często, jak wskazuje wysokość wykładnika”.

${\ displaystyle {\ początek {macierz} a ^ {- n} = 1: \ underbrace {a: a: a: \ dotsb: a} _ {n \ \ mathm {dzielniki}} \ koniec {matryca}}}$

Dla liczby rzeczywistej i naturalnej definiujemy: ${\ styl wyświetlania a}$${\ styl wyświetlania n}$

${\ displaystyle a ^ {- n}: = {\ frac {1} {a ^ {n}}}, \ quad a \ neq 0}$

Analogiczną definicję stosuje się również w bardziej ogólnym kontekście, gdy dostępne są elementy mnożenia i odwrotności , na przykład z macierzami odwracalnymi .

Wykładniki wymierne

Pozwolić liczbą wymierną z reprezentacją frakcji z . Dla każdego pozytywnego rzeczywistego definiuje się: ${\ styl wyświetlania q}$${\ displaystyle q = {\ tfrac {m} {n}}}$${\ displaystyle m \ in \ mathbb {Z}, \ n \ in \ mathbb {N}}$${\ styl wyświetlania a}$

${\ displaystyle a ^ {q} = a ^ {\ tfrac {m} {n}}: = {\ sqrt [{n}] {a ^ {m}}}}$ ${\ styl wyświetlania \ qquad}$(lub, co jest równoważne, )${\ displaystyle a ^ {\ tfrac {m} {n}}: = ({\ sqrt [{n}] {a}}) ^ {m}}$

Na przykład:

${\ displaystyle 2 ^ {3,1} = 2 ^ {31/10} = {\ sqrt [{10}] {2 ^ {31}}} = ({\ sqrt [{10}] {2}}) ^ {31}}$

Wartość potęgi nie zależy od wybranej reprezentacji ułamkowej .

Ta sama definicja dotyczy . Wynika z tego, że for trzyma i że for nie istnieje. ${\ styl wyświetlania a = 0}$${\ styl wyświetlania 0 ^ {q} = 0}$${\ styl wyświetlania q> 0}$${\ styl wyświetlania 0 ^ {q}}$${\ styl wyświetlania q <0}$

Jeżeli jeden pozwala korzeni z ujemnymi numerami z nieparzystych wykładników korzeniowe, to można przedłużyć tę definicję do negatywnych podstawy i wykładników tych racjonalnych których skrót frakcje mają nieparzystych mianownika . Obejmuje to również potęgi z ujemnymi podstawami i pełnymi wykładnikami, ponieważ w tym przypadku mianowniki są takie same . ${\ styl wyświetlania 1}$

W takim przypadku w obliczeniach mogą być użyte wszystkie ułamki z liczbami nieparzystymi . Jednak podczas korzystania z ułamków prostych , błędy mogą wystąpić. Na przykład: ${\ styl wyświetlania a <0}$${\ displaystyle a ^ {q}}$${\ displaystyle q = {\ tfrac {m} {n}}}$${\ styl wyświetlania n}$${\ styl wyświetlania n}$

${\ displaystyle -2 = (-8) ^ {1/3} = {\ sqrt [{3}] {-8}} = {\ sqrt [{9}] {(-8) ^ {3}}} \ neq {\ sqrt [{6}] {(-8) ^ {2}}} = 2}$

Rzeczywiste wykładniki

Funkcje wykładnicze 0,5 ^x , 2 ^x , e ^x i 10 ^x

Jeżeli , jest dowolną liczbą rzeczywistą i ciągiem liczb wymiernych, który jest zbieżny, to definiujemy: ${\ styl wyświetlania a> 0}$${\ styl wyświetlania r}$${\ styl wyświetlania (q_ {n})}$${\ styl wyświetlania r}$

${\ displaystyle a ^ {r}: = \ lim _ {n \ do \ infty} a ^ {q_ {n}}}$

Ta definicja jest poprawna; Oznacza to, że wartość graniczna zawsze istnieje i nie zależy od wyboru sekwencji . ${\ styl wyświetlania (q_ {n})}$

Na przykład jest równy granicy ciągu${\ styl wyświetlania 2 ^ {\ pi}}$ ${\ displaystyle 2 ^ {3}, \, 2 ^ {3 {,} 1}, \, 2 ^ {3 {,} 14}, \, \ kropki.}$

Definicja nie może być rozszerzona na przypadek, w którym w tym przypadku nie musi istnieć wartość graniczna lub różne wartości graniczne są wynikiem różnych wyborów sekwencji . ${\ styl wyświetlania a <0}$${\ styl wyświetlania (q_ {n})}$

Inna definicja jest możliwa przy użyciu naturalnej funkcji wykładniczej i logarytmu naturalnego :

${\ displaystyle a ^ {r}: = \ operatorname {exp} (r \ ln a)}$

W tym celu funkcję wykładniczą można zdefiniować poprzez jej rozszerzenie szeregów :

${\ displaystyle \ operatorname {exp} (x) = \ suma _ {n = 0} ^ {\ infty} {\ frac {x ^ {n}} {n!}}}$

Ogólnie rzecz biorąc, potęgi o podstawach nieujemnych są zatem zdefiniowane dla wszystkich rzeczywistych wykładników. W przeciwieństwie do tego, potęgi z ujemnymi podstawami są zdefiniowane tylko dla tych racjonalnych wykładników, których skrócone ułamki mają nieparzyste mianowniki. Należą do niego wszystkie potencje o ujemnych podstawach i całych wykładnikach. Potęgi liczb ujemnych z innymi wykładnikami rzeczywistymi można zdefiniować w obszarze liczb zespolonych , ale nie są one wartościami rzeczywistymi.

Pisownia techniczna

Jeśli pisanie w indeksie górnym nie jest możliwe (na przykład w tekście ASCII ), notacja jest często używana a^b(na przykład w Algol 60 , w kodzie źródłowym TeX lub w systemach algebry komputerowej, takich jak Maple ), okazjonalnie również a**b(na przykład w Fortran , Perl lub Python ). Ze względu na różne opcje definiowania obszarów podstawy i wykładnika Haskella dostępne są trzy operatory potęgowe: a^b, a^^bi a**b.

Potęgi dziesięciu są często reprezentowane przez e lub E w elektronicznym przetwarzaniu danych lub na wyświetlaczu w kalkulatorach kieszonkowych .
Często spotykana reprezentacja dla z. B. -299792458 = -2,99792458 · 10 ⁸

Prawa władzy

Aby nie przeciążać poniższej tabeli, rozważamy tylko potęgi o rzeczywistych podstawach, które nie są równe . Ale jeśli weźmiesz pod uwagę jedno z praw wymienionych poniżej z tylko dodatnimi wykładnikami, to jest ono również ważne dla potęg podstawy . Gdy mówimy o liczbach wymiernych z mianownikami parzystymi lub nieparzystymi, zawsze mamy na myśli mianowniki ich ułamków skróconych. ${\ styl wyświetlania 0}$${\ styl wyświetlania 0}$

${\ displaystyle a ^ {0} = 1}$	dla wszystkich ( zobacz poniżej komentarze na temat "zera do potęgi zera" ) ${\ styl wyświetlania a \ neq 0}$
${\ displaystyle a ^ {- r} = {\ frac {1} {a ^ {r}}}}$	dla każdego prawdziwego , jeśli jest;${\ styl wyświetlania r}$${\ styl wyświetlania a> 0}$ dla arbitralnych racjonalnych z nieparzystymi mianownikami, jeśli jest. ${\ styl wyświetlania r}$${\ styl wyświetlania a <0}$
${\ displaystyle a ^ {\ frac {m} {n}} = {\ sqrt [{n}] {a ^ {m}}} = ({\ sqrt [{n}] {a}}) ^ {m }}$	dla dowolnej liczby naturalnej i całkowitej, jeśli jest; dla każdego naturalnego dziwnego i pełnego, jeśli jest. ${\ styl wyświetlania n}$${\ styl wyświetlania m}$${\ styl wyświetlania a> 0}$ ${\ styl wyświetlania n}$${\ styl wyświetlania m}$${\ styl wyświetlania a <0}$
${\ displaystyle a ^ {r + s} = a ^ {r} \ cdot a ^ {s}}$	dla każdego prawdziwego , jeśli jest; dla arbitralnych racjonalnych z nieparzystymi mianownikami, jeśli jest. ${\ styl wyświetlania r, s}$${\ styl wyświetlania a> 0}$ ${\ styl wyświetlania r, s}$${\ styl wyświetlania a <0}$
${\ displaystyle a ^ {rs} = {\ frac {a ^ {r}} {a ^ {s}}}}$	dla każdego prawdziwego , jeśli jest; dla arbitralnych racjonalnych z nieparzystymi mianownikami, jeśli jest. ${\ styl wyświetlania r, s}$${\ styl wyświetlania a> 0}$ ${\ styl wyświetlania r, s}$${\ styl wyświetlania a <0}$
${\ displaystyle (a \ cdot b) ^ {r} = a ^ {r} \ cdot b ^ {r}}$	dla każdego naturalnego , a dla całości , jeśli ;${\ styl wyświetlania r}$${\ styl wyświetlania r}$${\ styl wyświetlania a \ cdot b \ neq 0}$ dla każdego prawdziwego , jeśli są; dla dowolnej liczby wymiernej z nieparzystymi mianownikami, jeśli przynajmniej jedna z liczb jest ujemna. ${\ styl wyświetlania r}$${\ styl wyświetlania a> 0, b> 0}$ ${\ styl wyświetlania r}$${\ styl wyświetlania a, b}$
${\ displaystyle \ po lewej ({\ frac {a} {b}} \ po prawej) ^ {r} = {\ frac {a ^ {r}} {b ^ {r}}}}$	dla każdego i całości, a jeśli , także ;${\ styl wyświetlania b \ neq 0}$${\ styl wyświetlania r}$${\ styl wyświetlania r \ leq 0}$${\ styl wyświetlania a \ neq 0}$ dla każdego prawdziwego , jeśli są; dla dowolnej liczby wymiernej z nieparzystymi mianownikami, jeśli przynajmniej jedna z liczb jest ujemna. ${\ styl wyświetlania r}$${\ styl wyświetlania a> 0, b> 0}$ ${\ styl wyświetlania r}$${\ styl wyświetlania a, b}$
${\ displaystyle (a ^ {r}) ^ {s} = a ^ {r \ cdot s}}$	dla każdej całości, jeśli jest; dla każdego prawdziwego , jeśli jest; dla każdego racjonalnego , z dziwnymi mianownikami, jeśli jest. ${\ styl wyświetlania r, s}$${\ styl wyświetlania a \ neq 0}$ ${\ styl wyświetlania r, s}$${\ styl wyświetlania a> 0}$ ${\ styl wyświetlania r, s}$${\ styl wyświetlania a <0}$

Jeśli przynajmniej jeden z wykładników jest nieracjonalne lub oba są racjonalne, ale ma przynajmniej jeden z numerów lub równej mianownika, a następnie jeden z wyrażeń lub jest za niezdefiniowany. W przeciwnym razie oba są zdefiniowane i albo zgadzają się, albo różnią się tylko znakiem . Dla any , if is i dla całości , if is, zawsze pasują. Te dwa przypadki są możliwe dla , a nie całkowite , ale racjonalne . To, który przypadek wystąpi, zależy od liczby dwójek w pierwszym rozkładzie licznika i mianownika . Aby rozpoznać poprawny znak po prawej stronie formuły wystarczy wstawić go do tej formuły . Znak, z którym jest wtedy ważny, pozostaje poprawny dla wszystkich i dany . Obowiązuje dla , a następnie obowiązuje dla wszystkich (a także dla , jeśli wszystkie wykładniki są dodatnie). ${\ styl wyświetlania r, s}$${\ styl wyświetlania r}$${\ styl wyświetlania r \ cdot s}$${\ styl wyświetlania (a ^ {r}) ^ {s}}$${\ displaystyle a ^ {r \ cdot s}}$${\ styl wyświetlania a <0}$${\ styl wyświetlania r, s}$${\ styl wyświetlania a> 0}$${\ styl wyświetlania r, s}$${\ styl wyświetlania a \ neq 0}$${\ styl wyświetlania a <0}$${\ styl wyświetlania r, s}$${\ styl wyświetlania r}$${\ style wyświetlania}$${\ displaystyle (a ^ {r}) ^ {s} = \ pm a ^ {r \ cdot s}}$${\ styl wyświetlania a = -1}$${\ styl wyświetlania a = -1}$${\ styl wyświetlania a <0}$${\ styl wyświetlania r, s}$${\ displaystyle (a ^ {r}) ^ {s} = - a ^ {r \ cdot s}}$${\ styl wyświetlania a <0}$${\ displaystyle (a ^ {r}) ^ {s} = | a | ^ {r \ cdot s}}$${\ styl wyświetlania a \ neq 0}$${\ styl wyświetlania a = 0}$

Na przykład i . Dlatego obowiązuje dla wszystkich, a więc dla wszystkich prawdziwych . ${\ displaystyle ((-1) ^ {2}) ^ {\ frac {1} {2}} = 1}$${\ displaystyle (-1) ^ {2 \ cdot {\ frac {1} {2}}} = - 1}$${\ displaystyle {\ sqrt {a ^ {2}}} = (a ^ {2}) ^ {\ frac {1} {2}} = - a ^ {2 \ cdot {\ frac {1} {2} }} = - a}$${\ styl wyświetlania a <0}$${\ displaystyle {\ sqrt {a ^ {2}}} = | a |}$${\ styl wyświetlania a}$

Potęgowanie nie jest ani przemienne , ponieważ na przykład uchwyty , ani asocjacyjne , ponieważ na przykład uchwyty . ${\ styl wyświetlania 2 ^ {3} = 8 \ nie = 9 = 3 ^ {2}}$${\ displaystyle \ lewy (3 ^ {1} \ prawy) ^ {3} = 27 \ neq 3 = 3 ^ {\ lewy (1 ^ {3} \ prawy)}}$

Notacja bez nawiasów oznacza, że potęgowanie jest prawostronne, patrz pierwszeństwo operatorów . ${\ displaystyle a ^ {b ^ {c}}}$${\ displaystyle a ^ {(b ^ {c})}}$

Potęgi liczb zespolonych

Dla wykładników całkowitych można zdefiniować potęgi o złożonych podstawach jak w przypadku rzeczywistym. Musisz jednak postępować inaczej dla każdego rzeczywistego lub złożonego wykładnika.

Pierwszym krokiem w definiowaniu potęg o podstawie zespolonej i wykładniku jest ciągłe rozszerzanie funkcji na zbiór liczb zespolonych. Można to zrobić na różne sposoby. Na przykład możesz wziąć numer ${\ styl wyświetlania e ^ {x}}$${\ styl wyświetlania \ mathbb {C}}$

${\ displaystyle e ^ {z} = \ suma _ {n = 0} ^ {\ infty} {\ frac {z ^ {n}} {n!}}}$

który zbiega się dla wszystkich i określa funkcję dla wszystkich . Za pomocą operacji na serii pierwszej udowadnia, że ${\ styl wyświetlania z \ w \ mathbb {C}}$${\ displaystyle z = x \ in \ mathbb {R}}$${\ styl wyświetlania e ^ {x}}$

${\ styl wyświetlania e ^ {z_ {1} + z_ {2}} = e ^ {z_ {1}} e ^ {z_ {2}}}$

dla dowolnego i wzoru Eulera${\ styl wyświetlania z_ {1}, z_ {2} \ w \ mathbb {C}}$

${\ displaystyle e ^ {i \, y} = \ cos y + i \, \ sin y}$

stosuje się do dowolnego . Wzór wynika z tego ${\ displaystyle y \ in \ mathbb {R}}$

${\ displaystyle e ^ {x + i \, y} = e ^ {x} \, (\ cos {y} + ja \, \ sin {y})}$,

które można również wykorzystać do definicji . Ta formuła pokazuje, że zbiór wartości jest taki sam , a funkcja ta jest okresowo z okresami , . ${\ styl wyświetlania e ^ {z}}$${\ styl wyświetlania e ^ {z}}$${\ displaystyle \ mathbb {C} \ setminus \ {0 \}}$${\ styl wyświetlania 2k \ pi i}$${\ displaystyle k \ in \ mathbb {Z}}$

Dlatego jego odwrotna funkcja jest niejednoznaczna i zdefiniowana dla wszystkich . Można go określić za pomocą wzoru , gdzie kwota, zbiór wartości argumentu i jest zwykłym logarytmem rzeczywistym . Główna wartość tej funkcji jest uzyskiwana przez użycie głównej wartości zamiast . Rzeczywistość jest ze zwykłej definicji , więc ta funkcja na zbiorze zgadza się ze zwykłym logarytmem rzeczywistym. ${\ styl wyświetlania \ nazwa operatora {Ln} (z)}$${\ styl wyświetlania z \ neq 0}$${\ styl wyświetlania \ nazwa operatora {Ln} (z) = \ ln | z | + i \ nazwa operatora {Arg} (z)}$${\ styl wyświetlania | z |}$${\ styl wyświetlania \ nazwa operatora {Arg} (z)}$${\ styl wyświetlania z}$${\ styl wyświetlania \ ln | z |}$${\ styl wyświetlania \ ln (z)}$${\ styl wyświetlania \ nazwa operatora {arg} (z)}$${\ styl wyświetlania \ nazwa operatora {Arg} (z)}$${\ styl wyświetlania z = x> 0}$${\ styl wyświetlania \ nazwa operatora {arg} (x) = 0}$${\ styl wyświetlania \ ln}$${\ styl wyświetlania \ mathbb {R} ^ {+}}$

Dla każdego z jednym definiuje się wtedy: ${\ styl wyświetlania a, z \ in \ mathbb {C}}$${\ styl wyświetlania a \ neq 0}$

${\ displaystyle a ^ {z} = e ^ {z \, \ operatorname {Ln} \, a}}$

Jest to również funkcja niejednoznaczna, której główna wartość wynika z użycia zamiast . ${\ styl wyświetlania \ ln}$${\ styl wyświetlania \ nazwa operatora {Ln}}$

Ale ta dwuznaczność znika i powstają zwykłe potęgi z całymi wykładnikami, które zostały zdefiniowane w pierwszej sekcji. Bądź i , a następnie narysuj reprezentację wykładniczą ${\ styl wyświetlania z = n \ in \ mathbb {Z}}$${\ styl wyświetlania a \ neq 0}$${\ displaystyle \ varphi \ in \ operatorname {Arg} (a)}$

${\ displaystyle a = | a | \, e ^ {i \ varphi}}$

po tym

${\ displaystyle a ^ {n} = | a | ^ {n} \, e ^ {w \ varphi}}$

ma zastosowanie.

Dla wymiernego wykładnika ze skróconą reprezentacją ułamka , z , potęga ma dokładnie różne wartości. Dotyczy to zwłaszcza . Jest nieparzyste i , to jest wśród nich dokładnie jedna liczba rzeczywista, a jest to liczba z podrozdziału 1.3. Jest parzysty i , a następnie nie przyjmuje wartości rzeczywistych. Ale jeśli jest parzysty i , to moc przyjmuje dokładnie dwie wartości rzeczywiste, które mają różne znaki. W tym przypadku dodatnia jest dokładnie taka sama jak liczba z sekcji 1.3. ${\ styl wyświetlania q}$${\ displaystyle q = {\ tfrac {m} {n}}}$${\ displaystyle m \ in \ mathbb {Z}, n \ in \ mathbb {N}}$${\ displaystyle a ^ {q}}$${\ styl wyświetlania n}$${\ displaystyle {\ sqrt [{n}] {a}} = a ^ {\ frac {1} {n}}}$${\ styl wyświetlania n}$${\ displaystyle a \ in \ mathbb {R}}$${\ displaystyle a ^ {q}}$${\ styl wyświetlania n}$${\ styl wyświetlania a <0}$${\ displaystyle a ^ {q}}$${\ styl wyświetlania n}$${\ styl wyświetlania a> 0}$${\ displaystyle a ^ {q}}$${\ displaystyle a ^ {q}}$

Jako przykład rozważ moc wysoką . ${\ styl wyświetlania i}$${\ styl wyświetlania i}$

Wyłącz i ${\ styl wyświetlania | i | = 1}$

${\ styl wyświetlania \ nazwa operatora {Arg} (i) = {\ frac {\ pi} {2}} + 2 {\ pi} k}$ z ${\ displaystyle k \ in \ mathbb {Z}}$

następuje

${\ displaystyle \ operatorname {Ln} (i) = i \ lewo ({\ frac {\ pi} {2}} + 2 {\ pi} k \ po prawej).}$

To skutkuje

${\ displaystyle ja ^ {i} = e ^ {i \ cdot ja ({\ frac {\ pi} {2}} + 2 \ pi k)} = e ^ {- {\ frac {\ pi} {2} } -2 \ pi k}}$ z ${\ displaystyle k \ in \ mathbb {Z}}$

Główna wartość odpowiada i jest taka sama${\ styl wyświetlania k = 0}$${\ displaystyle e ^ {- {\ frac {\ pi} {2}}}.}$

Specjalne moce

Uprawnienia całkowitą wynoszącą 10 (uprawnień dziesięć ) stanowią podstawę naszego systemu liczbowego , w systemie dziesiętnym . Zapisane jako moc, m.in. Na przykład ^10-9 dla 0,000000001 lub 10 ¹¹ dla 100 miliardów, są one używane w naukach przyrodniczych do reprezentowania bardzo dużych lub bardzo małych liczb dodatnich.

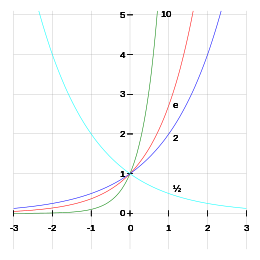
W matematyce i technice potęgi o podstawie , czyli liczbie Eulera, są nadal szczególnie ważne . ${\ displaystyle e \ ok 2 {,} 7182818284590452}$

Potęgi dwóch wynikają z wielokrotnego podwajania. Zaskakująco szybki wzrost liczb sprawia, że ​​potęgi dwóch są popularne w praktycznych przykładach:

• Arkusz papieru o zwykłym rozmiarze może być tylko od siedmiu do połowy rozmiaru zgięcia . Ma wtedy 128 warstw i tylko jedną 128 jego powierzchni. Gdyby można go było złożyć 42 razy, co jest możliwe tylko w teorii, jego grubość około 400 000 km odpowiadałaby mniej więcej odległości Ziemi od Księżyca .
• Każdy ma dwoje biologicznych rodziców, a większość ma czworo dziadków i ośmiu pradziadków. Bez utraty przodków , 70  pokoleń temu, w momencie narodzin Chrystusa, byliby to przodkowie , chociaż żyło wówczas mniej niż 10 ⁹ osób.${\ displaystyle 2 ^ {70} \ około 10 ^ {21}}$
• Legenda ziarna pszenicy od wynalazcy szachów, który podwoił liczbę ziaren pszenicy na każdym placu na szachownicy, ilustruje również gwałtowny wzrost potęgi dwójki.

Do cyfrowego przetwarzania danych na komputerze, który jest systemem binarnym używanym z bazą 2 Jednostki wielkości cyfrowych systemów pamięci masowej są zatem potęgami dwójki, tj. uprawnieniami do podstawy 2 (czyli 1, 2, 4, 8, 16, ...). Kibibyte (w skrócie kib) odpowiada bajtów . ${\ styl wyświetlania 2 ^ {10} = 1024}$

W piramidach finansowych , takich jak tak zwane kręgi Schenka , uruchamiane są niektóre systemy, które zapewniają nie tylko podwojenie, ale ośmiokrotny wzrost liczby nowych członków na krok. Takie konsekwencje rosną tak szybko, że systemy nieuchronnie załamują się już po kilku krokach. Często sugerowana przez inicjatorów stabilność piramid nie może istnieć. Dlatego są one zakazane w wielu krajach nie bez powodu.

Zero do zera

Analiza

Wykres funkcji dla i ze szczególnym uwzględnieniem sąsiedztwa , w którym (pionowa) prosta kończy się powierzchnia. Kolorowe krzywe pokazują różne przybliżenia (0; 0) z różnymi wartościami granicznymi dla .${\ styl wyświetlania z = x ^ {y}}$${\ styl wyświetlania x \ w [0,1]}$${\ styl wyświetlania y \ w [-1, + 1]}$${\ styl wyświetlania (0; 0; z)}$${\ styl wyświetlania 0 ^ {0}}$

Pytanie, czy i w jaki sposób można przypisać temu wyrażeniu unikalną wartość, zajmowało matematyków co najmniej od pierwszej połowy XIX wieku. ${\ styl wyświetlania 0 ^ {0}}$

Rysunek po prawej pokazuje w swojej trójwymiarowej reprezentacji wykresu funkcji, że dowolne wartości można osiągnąć poprzez odpowiedni dobór punktów aproksymacji do początku . Podobnie jak z. B. ${\ styl wyświetlania z = x ^ {y}}$${\ displaystyle z \ in \ mathbb {R} _ {\ geq 0}}$${\ styl wyświetlania (x; y)}$${\ styl wyświetlania (0; 0)}$

1. ${\ displaystyle \ lim _ {y \ do 0+} 0 ^ {y} = 0}$,
2. ${\ displaystyle \ lim _ {y \ do 0 +} {\ Bigl (} e ^ {- r ^ {- 2}} {\ Bigr)} ^ {y} = 0}$,
3. ${\ displaystyle \ lim _ {t \ to + \ infty} x ^ {y} = c}$
     z , i ,${\ styl wyświetlania 0 <c <1}$${\ styl wyświetlania x = c ^ {t}}$${\ displaystyle y = {\ tfrac {1} {t}}}$
4. ${\ displaystyle \ lim _ {x \ do 0+} x ^ {0} = 1}$ oraz
5. ${\ displaystyle \ lim _ {y \ do 0 -} {\ Bigl (} e ^ {- r ^ {- 2}} {\ Bigr)} ^ {y} = + \ infty}$.

Te przykłady pokazują, że funkcja odbiega w tym momencie , ponieważ wartość graniczna tego typu  oczywiście nie istnieje. ${\ styl wyświetlania z = x ^ {y}}$${\ styl wyświetlania (0; 0)}$${\ displaystyle \ textstyle \ lim _ {(x; y) \ do (0; 0)} \; x ^ {y}}$

Wyrażenie znajdujące się pod znakiem wartości granicznej, którego nie można obliczyć na podstawie zestawów wartości granicznych i właściwości ciągłości, nazywa się wyrażeniem nieokreślonym . Przykłady są również . To ostatnie wyrażenie wynika z obliczeń potęg, których podstawa i wykładnik są jednocześnie sprzeczne i nie można go określić, jeśli nie ma między nimi związku. ${\ displaystyle {\ tfrac {0} {0}}, \, {\ tfrac {\ infty} {\ infty}}}$${\ styl wyświetlania 0 ^ {0}}$${\ styl wyświetlania 0}$

Jako odpowiednia w okolicznościach oczywista wartość może (która jest na rysunku, linia prosta, ponieważ każda prawda) lub (belka, ponieważ jest prawdziwa) widok. Ale są też nowoczesne podręczniki do analizy, które wyraźnie pozostawiają władzę (w tej formie) niezdefiniowaną. ${\ styl wyświetlania 1}$${\ styl wyświetlania (x; 0; 1)}$${\ styl wyświetlania x ^ {0} = 1}$${\ displaystyle x \ in \ mathbb {R} ^ {\ razy}}$${\ styl wyświetlania 0}$${\ styl wyświetlania (0; + y; 0)}$${\ styl wyświetlania 0 ^ {y} = 0}$${\ displaystyle y \ in \ mathbb {R} ^ {+}}$${\ styl wyświetlania 0 ^ {0}}$

Do początku XIX wieku matematycy najwyraźniej stawiali zakłady bez bardziej szczegółowego kwestionowania tej definicji. Augustin-Louis Cauchy , jednak wymienione razem z innymi wyrażeniami jak w tabeli wyrażeń nieokreślonych. W 1833 Guillaume Libri opublikował pracę, w której przedstawił nieprzekonujące argumenty na rzecz , które później stały się kontrowersyjne. W obronie Libri August Ferdinand Möbius opublikował dowody od swojego nauczyciela Johanna Friedricha Pfaffa , które zasadniczo wykazały, że ma to  zastosowanie, i rzekome dowody,  które w  stosownych przypadkach dostarczyły. Poprawność tego dowodu była kontrprzykładem i szybko obalona. ${\ styl wyświetlania 0 ^ {0} = 1}$${\ styl wyświetlania 0 ^ {0}}$${\ styl wyświetlania 0/0}$${\ styl wyświetlania 0 ^ {0} = 1}$${\ displaystyle \ textstyle \ lim _ {x \ do 0+} x ^ {x} = 1}$${\ displaystyle \ textstyle \ lim _ {t \ do 0+} x (t) ^ {y (t)} = 1}$${\ displaystyle \ textstyle \ lim _ {t \ do 0+} x (t) = \ lim _ {t \ do 0+} y (t) = 0}$${\ styl wyświetlania x (t) = e ^ {- 1 / t}}$${\ styl wyświetlania y (t) = t}$

Donald E. Knuth wspomniał historię kontrowersji w American Mathematical Monthly w 1992 roku i stanowczo sprzeciwił się wnioskowi, że pozostaje on nieokreślony. Jeśli nie przyjmie się wartości 1 dla potęgi , wiele zdań matematycznych, takich jak twierdzenie dwumianowe , wymaga${\ styl wyświetlania 0 ^ {0}}$${\ styl wyświetlania 0 ^ {0}}$

${\ displaystyle (a + b) ^ {n} = \ suma _ {k = 0} ^ {n} {n \ wybierz k} a ^ {k} b ^ {nk}}$

specjalne traktowanie przypadków (na indeksie ) lub (na indeksie ) lub (na ). ${\ styl wyświetlania a = 0}$${\ styl wyświetlania k = 0}$${\ styl wyświetlania b = 0}$${\ styl wyświetlania k = n}$${\ styl wyświetlania a + b = 0}$${\ styl wyświetlania n = 0}$

Podobnie potęga występuje w szeregach potęgowych, takich jak dla funkcji wykładniczej${\ styl wyświetlania 0 ^ {0}}$

${\ displaystyle e ^ {t} = \ suma _ {n = 0} ^ {\ infty} {\ frac {t ^ {n}} {n!}}}$

dla indeksu lub we wzorze empirycznym na szereg geometryczny${\ styl wyświetlania t = 0}$${\ styl wyświetlania n = 0}$

${\ displaystyle \ sum _ {k = 0} ^ {n} q ^ {k} = {\ frac {1-q ^ {n + 1}} {1-q}}}$

dla na indeksie przed. Tu też pomaga konwencja . ${\ styl wyświetlania q = 0}$${\ styl wyświetlania k = 0}$${\ styl wyświetlania 0 ^ {0} = 1}$

Przytoczone zastosowania potęgi to (podobnie jak wiele innych podobnych) wypowiedzi o wielomianach, wielomianach lub szeregach potęgowych, w których wykładnik wyrazu jest stały 0, a podstawa – raczej wyjątkowo – może przyjąć wartość 0. We wszystkich tych przypadkach występujące terminy są ciągłymi sumami lub czynnikami, które mają wartość 1 dla elementów odwracalnych, których wartość można następnie łatwo (i całkowicie w sensie ) uzupełniać w sposób ciągły jako 1 dla luki . ${\ styl wyświetlania 0 ^ {0}}$${\ styl wyświetlania y}$${\ styl wyświetlania x ^ {y}}$${\ styl wyświetlania x}$${\ styl wyświetlania x}$${\ styl wyświetlania x \ do 0}$${\ styl wyświetlania 0 ^ {0} = 1}$

Knuth rozróżnia jednak i pisze: „Cauchy miał dobre powody, by uważać za niezdefiniowaną formę ograniczającą ” (na przykład w języku niemieckim: Cauchy miał dobre powody, by rozważać niezdefiniowane wyrażenie Limesa), przez co rozumie ograniczające procesy formy, w których zarówno podstawa i wykładnik dla pewnej wartości zbliżają się do 0 do woli. ${\ styl wyświetlania 0 ^ {0}}$${\ styl wyświetlania 0 ^ {0}}$ ${\ styl wyświetlania 0 ^ {0}}$${\ displaystyle \ lim x (t) ^ {y (t)}}$${\ styl wyświetlania x (t)}$${\ styl wyświetlania y (t)}$${\ styl wyświetlania t}$

Dzięki temu zastrzeżeniu D. E. Knutha proste przypadki wyrazów bezwzględnych w wielomianach i szeregach potęgowych są rozwiązywane natychmiast i w sposób ogólny, bez sprzeczności ze szczegółowym rozważeniem bardziej skomplikowanych procesów brzegowych.

Teoria mnogości

W teorii mnogości potęga dwóch zbiorów jest definiowana jako zbiór wszystkich funkcji od do , czyli jako zbiór zbiorów par uporządkowanych , tak że dla każdego istnieje dokładnie jedna z . Jeśli ktoś wskazuje na liczność o , to co uzasadnia zapis mocy dla zestawów dotyczy (dla zbiorów skończonych, ale także poza nią). Teraz jest dokładnie jedna funkcja zdefiniowana na pustym zbiorze , czyli zbiór par z powyższą właściwością, a mianowicie . Dlatego obowiązuje to , co pozostaje słuszne. ${\ styl wyświetlania B ^ {A}}$${\ styl wyświetlania A}$${\ styl wyświetlania B}$${\ styl wyświetlania f}$${\ styl wyświetlania (a, b)}$${\ displaystyle a \ w A}$${\ styl wyświetlania b \ w B}$${\ styl wyświetlania (a, b) \ w f}$${\ styl wyświetlania | A |}$${\ styl wyświetlania A}$${\ styl wyświetlania | B ^ {A} | = | B | ^ {| A |}}$${\ styl wyświetlania \ pusty zestaw}$${\ styl wyświetlania \ pusty zestaw}$${\ displaystyle B ^ {\ emptyset} = \ {\ emptyset \}}$${\ displaystyle B = \ emptyset}$

Liczby naturalne są definiowane rekurencyjnie w teorii mnogości w następujący sposób (patrz model liczb naturalnych von Neumanna ):

${\ displaystyle 0: = \ emptyset, \, 1: = \ {0 \} = \ {\ emptyset \}, \, 2: = \ {0,1 \} = \ {\ emptyset, \ {\ emptyset \ } \}, \, 3: = \ {0,1,2 \} = \ kropki}$

W związku z tym w teorii mnogości:

${\ displaystyle 0 ^ {0} = \ emptyset ^ {\ emptyset} = \ {\ emptyset \} = 1}$

Funkcje odwrotne

Ponieważ prawo przemienne nie ma zastosowania do potęgowania, istnieją dwie odwrotne operacje arytmetyczne:

• ekstrakcji z korzeni do rozwiązania równania zgodnie z jego konstrukcji, to znaczy określenia podstawy jeśli wykładnik jest znany${\ styl wyświetlania x ^ {a} = b}$${\ styl wyświetlania x}$
• biorąc do logarytmu do równania typu , to jest decydujące wykładnik kiedy podstawa jest podane.${\ displaystyle a ^ {x} = b}$

Uogólnienia

Bardziej ogólne podstawy

Ogólnie rzecz biorąc, w każdej półgrupie występują potęgi o dodatnich, całkowitych wykładnikach . Jeśli to ma element neutralny, a zatem staje się monoidem , wtedy wykładnik 0 również ma sens i zawsze jest elementem neutralnym. Prawa władzy mają zastosowanie do wszystkich${\ styl wyświetlania M}$${\ displaystyle a ^ {0}}$${\ styl wyświetlania a, b \ w M; m, n \ in \ mathbb {N} _ {0}}$

• ${\ displaystyle a ^ {m + n} = a ^ {m} \ cdot a ^ {n}}$
• ${\ styl wyświetlania (a ^ {m}) ^ {n} = a ^ {m \ cdot n}}$
• ${\ styl wyświetlania (a \ cdot b) ^ {m} = a ^ {m} \ cdot b ^ {m}}$jeśli i zamień, re. H. jeśli dotyczy.${\ styl wyświetlania a}$${\ styl wyświetlania b}$ ${\ styl wyświetlania ab = ba}$

Jeśli jest to element odwracalny , możesz użyć ${\ styl wyświetlania a}$

${\ displaystyle \! \ a ^ {- n} = (a ^ {- 1}) ^ {n}}$ dla ${\ displaystyle n \ in \ mathbb {N}}$

Zdefiniuj potęgi dowolnym wykładnikiem całkowitym. Analogicznie obowiązują zasady obliczania. W przypadku grup abelian , to wykazuje, że do wzmagania strukturze - moduł jest indukowany. ${\ styl wyświetlania \ mathbb {Z}}$

Bardziej ogólne wykładniki

Bardziej ogólne wykładniki, takie jak macierze, są zwykle rozważane tylko w połączeniu z bazą , tj. jako wartości uogólnionej funkcji wykładniczej . ${\ styl wyświetlania e}$

Ponadto notacja potęgowa jest czasami używana w przypadku innych naturalnych kontynuacji. Na przykład w algebraicznej teorii liczb czasami brane są pod uwagę potęgi elementów ( topologicznych ) grup Galois z wykładnikami w uzupełnieniach ; jest to wówczas jednoznacznie określona ciągła kontynuacja mapowania ${\ styl wyświetlania \ mathbb {Z}}$

${\ displaystyle \ mathbb {Z} \ do G, \ quad n \ mapsto g ^ {n}.}$

Dla dowolnych liczb kardynalnych i potęgę można zdefiniować przez, przy czym zbiór wszystkich funkcji oznaczamy przez zbiór pierwotny i zbiór obrazów .To uogólnienie zakłada aksjomat zbioru potęgi , przy czym aksjomat wyboru jest zwykle przyjmowany również do obsługi liczb kardynalnych . ${\ styl wyświetlania | X |}$${\ styl wyświetlania | Y |}$${\ displaystyle | Y | ^ {| X |}: = | Y ^ {X} |}$${\ styl wyświetlania Y ^ {X}}$${\ styl wyświetlania X}$${\ styl wyświetlania Y}$

Niejednoznaczność notacji wykładniczej

Notacja wykładnicza może mieć różne znaczenia, szczególnie dla funkcji , w zależności od tego, czy zapis ma odzwierciedlać iterację konkatenacji, czy mnożenie punkt po punkcie. Ponadto można również brać pod uwagę indeks górny. Z reguły to, co ma na myśli, wynika z kontekstu.

Powiązanie

Notacja potęgowa jest często używana jako skrót dla konkatenacji funkcji, których wartości znajdują się ponownie w zakresie definicji, na przykład dla iteracji w układach dynamicznych .

Jeden definiuje, gdzie id oznacza tożsamość w domenie, rekurencyjnie:

${\ displaystyle f ^ {0}: = \ mathrm {id}; \ quad f ^ {n}: = f \ circ f ^ {n-1}}$

dla , więc ${\ styl wyświetlania n \ geq 1}$

${\ displaystyle f ^ {1}: = f; \ quad f ^ {2}: = f \ circ f,}$

i tak dalej.

Oznacza to dla wartości funkcji

${\ displaystyle f ^ {0} (x) = \ mathrm {id} (x) = x; \ quad f ^ {1} (x) = f (x); \ quad f ^ {2} (x) = (f \ ok f) (x) = f (f (x))}$

i na ogół

${\ displaystyle f ^ {n} (x) = (f \ circ f ^ {n-1}) (x) = f \ lewo (f ^ {n-1} (x) \ prawo).}$

Jako rozszerzenie tej definicji, jest zazwyczaj definiowane jako funkcja odwrotna do . W szczególności ta notacja jest również na wielu kalkulatorach , na przykład, a poza tym istnieją odwrotne funkcje trygonometryczne z wyznaczonymi. Często oznacza również funkcję archetypu . ${\ styl wyświetlania f ^ {-1}}$${\ styl wyświetlania f}$ ${\ styl wyświetlania \ arcsin}$${\ styl wyświetlania \ grzech ^ {-1}}$${\ styl wyświetlania f ^ {-1}}$

mnożenie

Jako notację skróconą dla mnożenia kilku wartości funkcyjnych funkcji trygonometrycznych z tymi samymi argumentami, jak np. z twierdzeniami o addycji dla funkcji trygonometrycznych występują często, ma też znaturalizowany zapis potencji, czyli pisanie

${\ displaystyle \ sin ^ {2} \! x: = (\ sin x) ^ {2} = \ sin (x) \ cdot \ sin (x) = \ sin x \ cdot \ sin x}$.

Nie jest to zgodne z przedstawionym powyżej zapisem dotyczącym łączenia funkcji. To samo dotyczy wielomianów . Z jedynką zawsze oznacza iloczyn krotności nieokreślonego z samym sobą.Ponieważ nieokreślone jako funkcja wielomianowa jest identycznym odwzorowaniem, notacja potęgowa jako iteracja funkcji nie miałaby tutaj sensu. ${\ styl wyświetlania x ^ {n}}$${\ styl wyświetlania n}$${\ styl wyświetlania x}$

Napisany u góry

W przypadku wielkości indeksowanych indeks jest czasami zapisywany w indeksie górnym, tak aby formuły sprawiały wrażenie potęgowania. Dzieje się tak zwłaszcza w rachunku tensorowym , na przykład przy wyznaczaniu pól wektorowych w notacji współrzędnych lub przy indeksowaniu wielkości już zaindeksowanych, takich jak sekwencje ciągów.

Pochodzenie

Jeśli wykładnik jest napisany w nawiasach, zwykle rozumie się odpowiednią pochodną , a następnie oznacza -tą pochodną funkcji . ${\ styl wyświetlania f ^ {(n)}}$${\ styl wyświetlania n}$${\ styl wyświetlania f}$

W językach programowania

Notacja z wykładnikiem w indeksie górnym jest praktyczna i łatwa do odczytania w formułach pisanych odręcznie i przy składaniu , ale niepraktyczna w przypadku maszyn do pisania i terminali, w których wszystkie znaki w wierszu są na tym samym poziomie. Dlatego wiele języków programowania używa alternatywnych sposobów reprezentowania potęgi: ${\ styl wyświetlania x ^ {y}}$

• x ↑ y: ALGOL , Commodore BASIC
• x ^ y: BASIC , J , MATLAB , R , Microsoft Excel , TeX (i jego odgałęzienia), TI-Basic , bc (dla wykładników całkowitych), Haskell (dla nieujemnych wykładników całkowitych), Lua , ASP i większość systemów algebry komputerowej
• x ^^ y: Haskell (dla podstawy wymiernej i wykładników całkowitych), D
• x ** y: Ada , Bash , COBOL , Fortran , FoxPro , Gnuplot , OCaml , Perl , PHP , PL / I , Python , REXX , Ruby , SAS , Seed7 , Tcl , ABAP , Haskell (dla wykładników zmiennoprzecinkowych), Turing , VHDL , JavaScript
• x⋆y: APL
• (expt x y): Wspólne seplenienie
• x sup y : równ

W wielu językach programowania zamiast operatora mocy istnieje odpowiednia funkcja biblioteczna, na przykład pow(x,y)w C , Math.pow(x,y)w Javie lub JavaScript oraz Math.Pow(x,y)w C-Sharp .

powiązane tematy

• Funkcja wykładnicza jest zmienna funkcja wykładnik The funkcja moc z bazy zmiennych.
• Odpowiednie sekwencje to sekwencja geometryczna i sekwencja potęgowa .
• Potęgowanie binarny jest skutecznym sposobem wzmagania naturalnej wykładnikiem.
• Wieża moc jest mocy którego podstawa i / lub wykładnik jest sama w sobie moc.
• Rząd wielkości , notacja naukowa - do reprezentowania liczb za pomocą potęg.

linki internetowe

Wikibooks: Matematyka dla szkoły${\ displaystyle {\ kolor {niebieski fiolet} {\ początek {macierz} {\ mathbf {MATEMA} \ mu \ alfa T \ mathbb {R} ix} \ koniec {macierz}}}}$  - Powers

Indywidualne dowody

1. ↑ potencji. Bibliographisches Institut - Dudenverlag, dostęp 3 czerwca 2016 r . 
2. ↑ Kredyt tłumaczenie z greckiego d-namic, dynamis, który w starożytnej geometrii przynajmniej od Platon miał również znaczenie „kwadrat”.
3. ^ Składnia języka algorytmicznego Algol 60. ( Memento z 28 sierpnia 2012 w Internet Archive )
4. ↑ Odpowiedz na pytanie na Stackoverflow dotyczące operatorów mocy w Haskell
5. ↑ erab. autorstwa Günthera Reinelta. Z pomocą Carstena Kreutza: Lambacher Schweizer - Mathematik für die Fachhochschulreife / [Hauptbd.]. Całkowity zespół. Wydanie I. Klett-Schulbuchverlag, Stuttgart 2008, ISBN 978-3-12-732691-8 . 
6. ^ Augustin-Louis Cauchy: Analiza algébrique. Tabela z wyrażeniami nieokreślonymi znajduje się na stronie 69.
7. ↑ Guillaume Libri: Mémoire sur les fonctions kończy działalność . W: Journal for matematyki czystej i stosowanej , 10, 1833, s. 303-316.
8. ↑ August Ferdinand Möbius: Dowód równania , za JF Pfaff${\ styl wyświetlania 0 ^ {0} = 1}$ . W: Journal for matematyki czystej i stosowanej , 12, 1834, s. 134-136.
9. ↑ Donald E. Knuth : Dwie uwagi dotyczące notacji. W: Amerykański miesięcznik matematyczny. tom 99, nr. 5 maja 1992, s. 403-422; Preprint ( GZIP ; 26 kB) na stronie Knuth jako tekst źródłowy TeX ; arxiv : matematyka / 9205211 . Historia kontrowersji znajduje się na stronie 6 preprintu.
10. ↑ Możesz to zobaczyć na odwrót - z takim samym skutkiem na końcu: Pisownia jest „krótką formą” , która nie zawiera wykładnika 0. Uzgodniono, że wartość potęgi przyjmuje się jako 1, jeśli jej wykładnik staje się 0 poprzez konstelację zmiennych biegnących .${\ styl wyświetlania \ styl tekstu \ suma _ {k = 0} ^ {n} {n \ wybierz k} a ^ {k} b ^ {nk}}$${\ displaystyle \ textstyle a ^ {n} + \ suma _ {k = 1} ^ {n-1} {n \ wybierz k} a ^ {k} b ^ {nk} + b ^ {n}}$
11. ↑ Thomas Jech : Teoria mnogości . Springer-Verlag, 2003, ISBN 3-540-44085-2 , s. 28, równania (3.3)
12. ↑ Brian W. Kernighan, Lorinda L. Cherry: Matematyka składu — Podręcznik użytkownika . Wydanie II. 1978, s. 2 (angielski, kohala.com ).