pięciokąt

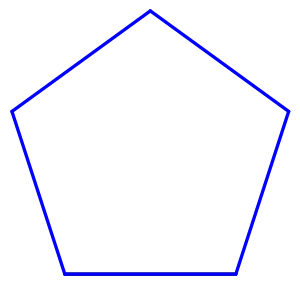
Pięciokąt regularny

Pięciokąta, także Pentagon (od starożytnego greckiego πεντάγωνον pentágōnon "pięciokąta") to figura geometryczna . Należy do grupy wielokątów ( wielokątów ) i jest definiowana przez pięć zdefiniowanych punktów .

Klasyfikacja

Pentagony, podobnie jak wszystkie wielokąty niebędące trójkątami , można podzielić na:

• Odwrócony pięciokąt: przecinają się co najmniej dwa boki.
• pięciokąt wklęsły: co najmniej jeden kąt wewnętrzny jest większy niż 180 °. Pięciokąt może mieć maksymalnie dwa takie kąty .
• pięciokąt wypukły: wszystkie kąty wewnętrzne są mniejsze niż 180 °
• Pięciokąt akordowy: wszystkie rogi leżą na wspólnym obwodzie .
• Regularny pięciokąt: wszystkie boki mają tę samą długość, a wszystkie wewnętrzne kąty mają ten sam rozmiar. Regularne pięciokąty mogą być wypukłe lub odwrócone.

Pięciokąt ogólny

kąt

Suma wewnętrznych kątów regularnego pięciokąta 540 °, to jest 3 razy 180 °, a wyniki z ogólnego wzoru na wielokątów , w którym liczba punktów narożnych wielokąta musi być stosowane dla zmiennej (w tym przypadku ) ${\ displaystyle n}$${\ displaystyle n = 5}$

${\ displaystyle \ sum {\ alpha =} (n-2) \ cdot 180 ^ {\ circ} = 3 \ cdot 180 ^ {\ circ} = 540 ^ {\ circ}}$

powierzchnia

Płaski pięciokąt ma jasno określoną powierzchnię , którą zawsze można obliczyć , dzieląc ją na trójkąty .

Pięciokąt regularny

Formuły

Wzory matematyczne na pięciokąt foremny
Powierzchnia	${\ Displaystyle A = {\ Frac {a ^ {2}} {4}} \ cdot {\ sqrt {25 + 10 \ cdot {\ sqrt {5}}}} \ około 1 {,} 720 \ cdot a ^ {2}}$
wysokość	${\ displaystyle h = r_ {u} + r_ {i} = {\ frac {a} {2}} \ cdot {\ sqrt {5 + 2 \ cdot {\ sqrt {5}}}} \ około 1 {, } 539 \ cdot a}$
Długość przekątnych	${\ Displaystyle d = {\ Frac {a} {2}} \ cdot (1 + {\ sqrt {5}}) \ około 1 {,} 618 \ cdot a}$
Wpisany promień	${\ displaystyle r_ {i} = {\ Frac {a} {10}} \ cdot {\ sqrt {25 + 10 \ cdot {\ sqrt {5}}}} \ około 0 {,} 688 \ cdot a}$
Promień obwodu	${\ displaystyle r_ {u} = {\ Frac {a} {10}} \ cdot {\ sqrt {50 + 10 \ cdot {\ sqrt {5}}}} \ około 0 {,} 851 \ cdot a}$
Kąt wewnętrzny	${\ Displaystyle \ alpha = 108 ^ {\ circ}}$

Pomoc wizualna do wyprowadzania sąsiednich stwierdzeń dotyczących kątów

Kąt wewnętrzny

Kąt , że dwa sąsiednie boki otaczają płaskie, pięciokąta foremnego (znowu zgodnie z ogólnym regularnych wielokątów )

${\ Displaystyle \ alpha = {\ Frac {(n-2)} {n}} \ cdot 180 ^ {\ circ} = {\ Frac {3} {5}} \ cdot 180 ^ {\ circ} = 108 ^ {\ circ}}$

powierzchnia

Pole A pięciokąta foremnego o długości boku jest pięciokrotnie większe od pola trójkąta rozpiętego przez jego środek i dwa punkty narożne. ${\ displaystyle a}$

${\ Displaystyle A = 5 \ cdot {\ Frac {1} {2}} \ cdot a \ cdot \ tan 54 ^ {\ circ} \ cdot {\ Frac {a} {2}} = {\ Frac {5} {4}} \ cdot a ^ {2} \ cdot \ tan 54 ^ {\ circ} \ około 1 {,} 720 \ cdot a ^ {2}}$

Generalnie z promieniem r _u

${\ Displaystyle A = {\ Frac {5} {8}} \ cdot r_ {u} ^ {2} \ cdot {\ sqrt {10 + 2 \ cdot {\ sqrt {5}}}}}$

lub

${\ Displaystyle A = {\ Frac {5} {2}} \ cdot r_ {u} ^ {2} \ cdot \ sin {72 ^ {\ circ}} \ około 2 {,} 378 \ cdot r_ {u} ^ {2}}$

Długość boku

${\ Displaystyle a = 2 \ cdot r_ {u} \ cdot \ sin 36 ^ {\ circ}}$

lub:

${\ displaystyle a = r_ {u} \ cdot {\ sqrt {\ frac {5 - {\ sqrt {5}}} {2}}} \ około 1 {,} 176 \ cdot r_ {u}}$

Informacje na temat konwersji można znaleźć w sekcji dotyczącej wartości sinus i cosinus, które można określić jako pierwiastki kwadratowe .

Złoty podział w pięciokącie

Pentagram

Pięciokąt regularny i pentagram tworzą podstawową figurę, w której relacja złotego podziału występuje wielokrotnie. Bok pięciokąta jest w złotym stosunku do jego przekątnych . Przekątne są ponownie podzielone w złotym stosunku, tj. H. AD jest do BD tak, jak BD do CD .

Dowód wykorzystuje podobieństwo wybranych trójkątów .

Każdy bok pięciokąta jest w złotym stosunku do każdej z dwóch sąsiednich przekątnych.

Przekątne mają złoty podział.

Konstrukcja z kompasem i linijką na zadany obwód

Budowa pięciokąta w zamkniętym kole

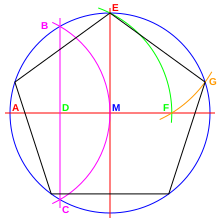
W przypadku pięciokąta foremnego istnieje matematycznie dokładna konstrukcja służąca do określania długości boku (patrz ilustracja).

1. Narysuj okrąg (później obwód , niebieski) o promieniu r wokół punktu środkowego M.
2. Narysuj dwie średnice (czerwone), które są do siebie prostopadłe .
3. Zmniejsz o połowę promień (magenta, punkt D).
4. Narysuj okrąg (zielony) z promieniem DE wokół punktu D. Przecina on prostą AM w punkcie F. Odcinek EF to długość boku.
5. Aby usunąć ten obszar, narysuj kolejny łuk (pomarańczowy) z promieniem EF wokół E. Przecina pierwsze kółko (niebieskie) w G. Powtórz odpowiednio proces.

Kalkulacja dla budowy:

${\ displaystyle {\ overline {EM}} = r \ cdot 1}$

${\ displaystyle {\ overline {DM}} = r \ cdot {\ frac {1} {2}}}$

${\ Displaystyle {\ overline {DE}} = r \ cdot {\ sqrt {1+ \ lewo ({\ Frac {1} {2}} \ prawej) ^ {2}}} = r \ cdot {\ frac { \ sqrt {5}} {2}}}$

${\ Displaystyle {\ overline {MF}} = r \ cdot \ lewo ({\ Frac {\ sqrt {5}} {2}} - {\ Frac {1} {2}} \ prawej) = r \ cdot { \ frac {{\ sqrt {5}} - 1} {2}}}$

${\ Displaystyle {\ overline {EF}} = r \ cdot {\ sqrt {1+ \ lewo ({\ Frac {{\ sqrt {5}} - 1} {2}} \ prawej) ^ {2}}} }$

Przekształcenie współczynnika:

${\ Displaystyle {\ Frac {\ overline {EF}} {r}} = {\ sqrt {1 + {\ Frac {5-2 \ cdot {\ sqrt {5}} + 1} {4}}}} = {\ sqrt {{\ frac {4} {4}} + {\ frac {5-2 \ cdot {\ sqrt {5}} + 1} {4}}}}}$

${\ Displaystyle {\ Frac {\ overline {EF}} {r}} = {\ sqrt {\ Frac {4 + 5-2 \ cdot {\ sqrt {5}} + 1} {4}}} = {\ sqrt {\ frac {10-2 \ cdot {\ sqrt {5}}} {4}}}}$

${\ displaystyle {\ frac {\ overline {EF}} {r}} = {\ sqrt {\ frac {5 - {\ sqrt {5}}} {2}}}}$

Odpowiada to dokładnie współczynnikowi w powyższym wzorze na długość boku .

Boki trójkąta MFE ( niepokazanego) odpowiadają dokładnie długościom boków sześciokąta foremnego ( ME ), pięciokąta foremnego ( EF ) i dziesięciokąta foremnego ( FM ) o danym promieniu obwodowym r.

Konstrukcja z cyrkiel i linijką o zadanej długości boku

Przy stosowaniu złotego podziału , zewnętrznego podziału

Pentagon o określonej długości boku

1. Narysować linię AB , która jest długość danego boku pięciokąta.
2. Zwiększ odległość od punktu A o około trzy czwarte odległości AB .
3. Narysuj łuk wokół punktu B o promieniu AB .
4. Narysuj łuk wokół punktu A o promieniu AB , wynikiem jest punkt przecięcia F.
5. Opuść prostopadle z punktu F do odcinka AB z punktem bazowym G.
6. Narysuj równolegle do linii FG od punktu A do łuku kołowego wokół punktu A, co spowoduje przecięcie punktu H.
7. Narysuj łuk wokół punktu G o promieniu GH do przedłużenia odcinka AB , punktu przecięcia J.
8. Narysuj łuk wokół punktu B z promieniem BJ do pionu przechodzącego przez punkt F, punkty przecięcia D na pionie i E z łukiem wokół punktu A.
9. Narysuj łuk wokół punktu D z promieniem BA, aż przecina łuk wokół punktu B, co daje punkt przecięcia C.
10. Połącz punkty BCDEA, uzyskuje się regularny pięciokąt.

Wniosek

Podobnie jak w konstrukcji o danym obwodzie decydującym elementem jest złoty podział .

Dla porównania wariantów konstrukcyjnych oznaczenia punktowe uzupełniono o wskaźniki: u dla konstrukcji o zadanym obwodzie, s dla konstrukcji o zadanej długości boku.

1. Strona pięciokąta:
   ${\ displaystyle {\ overline {E_ {u} F_ {u}}} \; {\ widehat {=}} \; {\ overline {A_ {s} B_ {s}}}}$
2. Promień dla złotego podziału:
   ${\ displaystyle {\ overline {D_ {u} E_ {u}}} \; {\ widehat {=}} \; {\ overline {G_ {s} H_ {s}}}}$
3. Warunki trasowe złotej sekcji:
   ${\ displaystyle \ Phi = {\ frac {\ overline {A_ {u} F_ {u}}} {\ overline {A_ {u} M_ {u}}}} = {\ frac {\ overline {A_ {u} M_ {u}}} {\ overline {M_ {u} F_ {u}}}} \; \; \; = \; \; \; {\ frac {\ overline {B_ {s} J_ {s}} } {\ overline {A_ {s} B_ {s}}}} = {\ frac {\ overline {A_ {s} B_ {s}}} {\ overline {A_ {s} J_ {s}}}} \ ; \; \; = \; \; \; {\ frac {1 + {\ sqrt {5}}} {2}} \ około 1 {,} 618}$

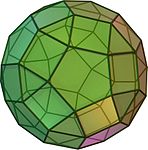
Wielościan z regularnymi pięciokątami

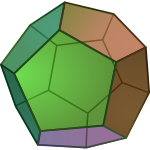
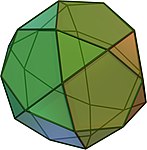
Dwunastościan jest jedynym wielościan foremny , który ma regularne pięciokątów jak powierzchniach bocznych . Niektóre Archimedesa stałe również zawierać regularnych pięciokątów, a mianowicie icosidodecahedron The obcięty Icosahedron The dwudziesto-dwunastościan rombowy mały i fazowane dwunastościan .

• 

  Dwunastościan

• 

  Icosidodecahedron

• 

  Dwudziestościan ścięty (korpus piłkarski)

• 

  Rhombicosidodecahedron

• 

  Skośny dwunastościan

Składanie papieru

Ściągając odręczny węzeł wykonany z paska papieru , przybiera kształt regularnego pięciokąta.

Wiązany pasek papieru

Parkiet z pięciokątami

15 rodzajów płytek poziomych z przystającymi , wypukłymi pięciokątami

Jest tylko 15 różnych pięciokątów, za pomocą których można układać kafelki bez przerw, jeśli używany jest tylko jeden rodzaj płytek. Francuski matematyk Michaël Rao udowodnił to dopiero w 2017 roku.

Występowanie

Natura

Owoce okry

Pokrojone owoce gwiazdki

Okra , jak również gwiazda owoce mają kształt pięciokąta w przekroju. Kwiaty powoju są również pięciokątne. Również rozgwiazdy i kruche gwiazdy mają pięcioramienną symetrię. Wiele związków cyklicznych zawiera pięcioczłonową strukturę pierścieniową (np. Cyklopentan , γ-butyrolakton , furan , furanozy itp.).

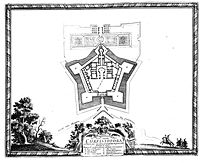
Architektura i budowa fortec

Plan piętra nowoczesnej twierdzy bastionowej ma często kształt pięciokąta. Tak więc regularne pięciokąty to całkowicie odbudowana twierdza Bourtange w Holandii, a także Nyenschanz (dziś w Sankt Petersburgu ), cytadela Jaca , cytadela w Pampelunie , twierdza Dömitz , cytadela Turynu , cytadela 's-Hertogenbosch , cytadela Strasburga , cytadela Amiens , cytadela Vitry-le-François autorstwa Girolamo Mariniego , która została zburzona w 1598 roku , cytadela w Antwerpii , cytadela Doullens (Pikardia, tylko częściowo na regularnym planie) , cytadela w Lille , zamek Harburg , cytadela Vechta , cytadela w Munster , fort Nieuw-Amsterdam , fort w Kopenhadze , fort Tilbury w Essex na wschód od Londynu , twierdza na wyspie Poel w Meklemburgii, twierdza Wülzburg w pobliżu Weissenburga w Bawarii i twierdza Goryōkaku w Japonii.

Typ pałacu obronnego (Palazzo in fortezza) z regularnym pięciokątnym planem reprezentuje Villa Farnese , zamki Krzyżtopór i Nowy Wiśnicz oraz fortyfikacje zamku w Łańcucie w Polsce. Miasto Sathmar w dzisiejszej Rumunii posiadało pięciokątną fortecę.

Siedziba Departamentu Obrony Stanów Zjednoczonych w Waszyngtonie nazywana jest Pentagonem ze względu na jej regularny kształt pięciokąta .

Budynki sakralne, takie jak kościół Korwina w Hanowerze, kościół Dietricha Bonhoeffera (Kolonia-Lindenthal) , kościół pielgrzymkowy Zelená Hora w Czechach czy kościół św. Michała w Detmold (Westfalia) oparte są na pięcioboku .

Konstrukcje wieżowe, takie jak stalowa wieża komunikacyjna na Potsdamer Platz lub drewniana wieża widokowa na Hohenmirsberger Platte, są wznoszone na pięciokątnym przekroju .

Pięciokątny kamień jest kamień graniczny w Dolnej Austrii.

• 

  Cytadela w Lille

• 

  Plan piętra Palazzo Farnese w Caprarola

• 

  Zamek Krzyżtopór

• 

  Twierdza na wyspie Poel

• 

  Zdjęcie satelitarne Pentagonu

• 

  Goryōkaku

Zobacz też

Pentagon zgodnie z twierdzeniem Mascheroniego, utworzony za pomocą samej pary kompasów

linki internetowe

Wikisłownik: Pentagon  - wyjaśnienia znaczeń, pochodzenie słów, synonimy, tłumaczenia

Indywidualne dowody

1. ^ C. Stanley Ogilvy: Entertaining Geometry. Rozdział 9: Złoty podział - 9.1 Pentagram. Vieweg + Teubner Verlag, Wiesbaden 1984, ISBN 3-528-28314-9 , s. 76-77, doi: 10.1007 / 978-3-663-00104-1_10 .
2. ^ M. Rao: Wyczerpujące poszukiwanie wypukłych pięciokątów pokrywających płaszczyznę. 1 sierpnia 2017 r., Arxiv : 1708.00274
3. ^ Matthias Schütte, Christoph Drösser: Puzzle kafelkowe. W: czas . Nr 32/2017, s. 36.