pierwiastek kwadratowy

Wykres funkcji pierwiastka kwadratowego ${\ displaystyle y = {\ sqrt {x}}}$

W reprezentacji logarytmicznym wykres funkcji pierwiastka kwadratowego staje się linię prostą o nachyleniu  ¹ / ₂ .

Pierwiastkowa (potocznie korzeniowego angielski pierwiastek , tak sqrt ) numer nieujemne , że (jednoznacznie wyznaczone) Numer nieujemne, której kwadrat jest równa ustalonej ilości IS. Symbolem pierwiastka kwadratowego jest znak pierwiastka kwadratowego , więc pierwiastek kwadratowy z liczby jest reprezentowany przez. Liczba lub termin znajdujący się pod korzeniem nazywa się radicand . Bardziej szczegółowy zapis jest mniej powszechny.Ponadto pierwiastek kwadratowy można wyrazić jako potęgę : jest równoważny na przykład, ponieważ i pierwiastek kwadratowy z jest równy . ${\ displaystyle y}$${\ displaystyle y}$ ${\ displaystyle {\ sqrt {}}}$${\ displaystyle y}$${\ displaystyle {\ sqrt {y}}}$ ${\ displaystyle y}$${\ displaystyle {\ sqrt {y}}}$${\ displaystyle {\ sqrt [{2}] {y}}.}$${\ Displaystyle y ^ {\ Frac {1} {2}}}$${\ displaystyle {\ sqrt {y}}.}$${\ Displaystyle 3 ^ {2} = 3 \ cdot 3 = 9}$${\ displaystyle 3 \ geq 0}$${\ displaystyle 9}$${\ displaystyle 3}$

Ponieważ równanie ma dla dwóch rozwiązań , pierwiastek kwadratowy jest zwykle definiowany jako nieujemna z dwóch rozwiązań; Oznacza to , że zawsze ma zastosowanie, co oznacza, że ​​pojęcie pierwiastka kwadratowego jest jednoznaczne. Dwa rozwiązania równania to zatem i${\ Displaystyle x ^ {2} = y}$${\ displaystyle y> 0}$${\ displaystyle {\ sqrt {y}} \ geq 0.}$${\ displaystyle x_ {1} = {\ sqrt {y}}}$${\ displaystyle x_ {2} = - {\ sqrt {y}}.}$

Wstępna uwaga dotycząca definicji

Podczas formalnego definiowania pierwiastka kwadratowego należy wziąć pod uwagę dwa problemy:

• Jeśli ograniczysz się do nieujemnych liczb wymiernych , w wielu przypadkach pierwiastek kwadratowy jest niezdefiniowany. Już w starożytności odkryto, że liczba, na przykład, nie może być liczbą wymierną (patrz dowód irracjonalności pierwiastka z 2 ).${\ displaystyle {\ sqrt {2}}}$
• Ogólnie rzecz biorąc, istnieją dwie różne liczby, których kwadraty pasują do podanej liczby. Na przykład ze względu na liczbę byłby potencjalnym kandydatem na pierwiastek kwadratowy .${\ Displaystyle (-3) ^ {2} = (- 3) \ cdot (-3) = 9}$${\ displaystyle -3}$${\ displaystyle 9}$

Symbol dla pierwiastka kwadratowego został użyty po raz pierwszy w ciągu 16 wieku . Uważa się, że znak jest zmodyfikowaną formą małej litery r , która jest skrótem od łacińskiego słowa „radix” (rdzeń). Pierwotnie symbol znajdował się przed radicand; brakowało poziomego przedłużenia. Dlatego też Carl Friedrich Gauß nadal używał nawiasów dla bardziej złożonych wyrażeń źródłowych i pisał na przykład zamiast${\ Displaystyle {\ sqrt {}} (b ^ {2} -4ac)}$${\ Displaystyle {\ sqrt {b ^ {2} -4ac}}.}$

W języku angielskim pierwiastek kwadratowy nazywa się „pierwiastkiem kwadratowym”, dlatego termin „sqrt” jest używany na określenie funkcji pierwiastka kwadratowego w wielu językach programowania .

Pierwiastki kwadratowe liczb rzeczywistych

Wykres funkcji kwadratowej (czerwony i niebieski). Poprzez odbicie tylko niebieskiej połowy na dwusiecznej pierwszej ćwiartki, tworzony jest wykres funkcji pierwiastka kwadratowego (zielony).

Definicja: Pierwiastek kwadratowy z nieujemnej liczby rzeczywistej to nieujemna liczba rzeczywista, której kwadrat jest równy . ${\ displaystyle {\ sqrt {y}}}$ ${\ displaystyle y}$${\ displaystyle x}$${\ Displaystyle x ^ {2} = x \ cdot x}$${\ displaystyle y}$

Równoważnie z tym, rzeczywisty pierwiastek kwadratowy można zdefiniować jako funkcję w następujący sposób: Niech

${\ Displaystyle {\ rozpocząć {wyrównane} q \ dwukropek [0; \ infty {[} & \ rightarrow [0; \ infty {[} \\ x & \ mapsto y = x ^ {2} \ koniec {wyrównane}} }$

(bijektywne) ograniczenie funkcji kwadratowej do zbioru nieujemnych liczb rzeczywistych. Odwrotność tej funkcji nazywamy funkcją pierwiastka kwadratowego${\ displaystyle q}$${\ displaystyle y \ mapsto x = {\ sqrt {y}}.}$

Uwagi

• Należy zauważyć, że funkcja kwadratowa wyjaśniona przez jest zdefiniowana dla wszystkich liczb rzeczywistych, ale nie jest odwracalna. Nie jest ani iniekcyjna, ani surjektywna .${\ Displaystyle \ mathbb {R} \ rightarrow \ mathbb {R}; x \ mapsto x ^ {2}}$
• Ograniczenie funkcji kwadratowej jest odwracalne i jest odwracane przez rzeczywistą funkcję pierwiastkową. Ponieważ tylko nieujemne liczby rzeczywiste pojawiają się jako obrazy , rzeczywista funkcja pierwiastka jest definiowana tylko dla tych liczb.${\ displaystyle q}$${\ displaystyle q}$
• Ze względu na ograniczenie wprowadzone przed odwróceniem liczb rzeczywistych z na nieujemne wartości funkcji pierwiastka kwadratowego są liczbami nieujemnymi. Ograniczenie funkcji kwadratowej do innych podzbiorów , w których różne liczby rzeczywiste mają zawsze różne kwadraty, prowadziłoby do innych funkcji odwrotnych, ale nie są one nazywane rzeczywistymi funkcjami pierwiastkowymi.${\ displaystyle q}$${\ displaystyle \ mathbb {R}}$

Przykłady

Pierwiastek kwadratowy z liczby naturalnej jest liczbą całkowitą lub niewymierną. Dowód jest analogiczny do dowodu irracjonalności pierwiastka 2 u Euklidesa .

Właściwości i zasady obliczania

Właściwości funkcji pierwiastka kwadratowego wynikają z właściwości funkcji kwadratowej ograniczonej do zbioru nieujemnych liczb rzeczywistych:

• ${\ displaystyle {\ sqrt {a \ cdot b}} = {\ sqrt {a}} \ cdot {\ sqrt {b}} \;}$dla .${\ Displaystyle \; 0 \ równoważnik a \, 0 \ równoważnik b}$
• ${\ displaystyle {\ sqrt {a \ cdot b}} = {\ sqrt {-a}} \ cdot {\ sqrt {-b}} \;}$dla .${\ Displaystyle \; a \ równoważnik 0, \, b \ równoważnik 0}$
• ${\ displaystyle 0 \ leq a <b \; \ Longleftrightarrow \; 0 \ równoważnik {\ sqrt {a}} <{\ sqrt {b}}}$, d. tj. funkcja pierwiastka kwadratowego ściśle rośnie.
• ${\ Displaystyle {\ sqrt {a ^ {2}}} = | a |}$trzyma z rzeczywistą kwotą dla dowolnych liczb rzeczywistych .${\ displaystyle a}$
• Z drugiej strony dotyczy tylko rzeczy nieujemnych .${\ displaystyle ({\ sqrt {a}}) ^ {2} = a}$${\ displaystyle a}$
• Funkcja pierwiastka kwadratowego jest różniczkowalna na , obowiązuje .${\ displaystyle \ mathbb {R} _ {+}}$ ${\ Displaystyle {\ Frac {\ mathrm {d} {\ sqrt {x}}} {\ mathrm {d} x}} = {\ Frac {1} {2 {\ sqrt {x}}}}}$
• W punkcie 0 nie jest różniczkowalna, jej diagram ma prostopadłą styczną z tamtym równaniem .${\ displaystyle x = 0}$
• Może być integrowalna metodą Riemanna w każdym zamkniętym podzakresie jego domeny , jedną z jego funkcji pierwotnych jest .${\ displaystyle [a, b]}$${\ Displaystyle F (x) = {\ tfrac {2} {3}} \ cdot {\ sqrt {x ^ {3}}}}$

Obliczanie pierwiastków kwadratowych z liczb rzeczywistych

Racjonalne przybliżone wartości kilku pierwiastków kwadratowych

${\ displaystyle {\ begin {tablica} {ccccr} {\ sqrt {2}} & \ ok i {\ sqrt {\ frac {49} {25}}} & = i {\ frac {7} {5}} \\ {\ sqrt {2}} & \ approx & {\ sqrt {\ frac {289} {144}}} & = & {\ frac {17} {12}} \\ {\ sqrt {2}} & \ approx & {\ sqrt {\ frac {1681} {841}}} & = & {\ frac {41} {29}} \\ {\ sqrt {3}} & \ ok & {\ sqrt {\ frac { 49} {16}}} & = & {\ frac {7} {4}} \\ {\ sqrt {3}} & \ ok & {\ sqrt {\ frac {361} {121}}} & = & {\ frac {19} {11}} \\ {\ sqrt {5}} & \ approx & {\ sqrt {\ frac {81} {16}}} & = & {\ frac {9} {4}} \\ {\ sqrt {6}} & \ approx & {\ sqrt {\ frac {2401} {400}}} & = & {\ frac {49} {20}} \\ {\ sqrt {7}} & \ approx & {\ sqrt {\ frac {64} {9}}} & = & {\ frac {8} {3}} \\ {\ sqrt {8}} & \ ok & {\ sqrt {\ frac { 289} {36}}} & = & {\ frac {17} {6}} \\ {\ sqrt {10}} & \ ok & {\ sqrt {\ frac {361} {36}}} & = & {\ frac {19} {6}} \\ {\ sqrt {11}} & \ approx & {\ sqrt {\ frac {100} {9}}} & = & {\ frac {10} {3}} \ end {tablica}}}$

Nawet jeśli należy wziąć pierwiastek kwadratowy z liczby naturalnej , wynikiem jest często liczba niewymierna , której rozszerzenie ułamka dziesiętnego jest zatem nieokresowym, niekońcowym ułamkiem dziesiętnym (a mianowicie dokładnie wtedy, gdy wynik nie jest naturalny) . Obliczanie pierwiastka kwadratowego, co nie jest liczbą wymierną jest zatem, aby ustalić przybliżoną wartość wystarczającą dokładnością. Można to zrobić na kilka sposobów:

Pisemne usuwanie korzeni

Jest to algorytm podobny do powszechnie stosowanej metody pisemnego dzielenia.

Zagnieżdżanie interwałowe

Ta procedura jest dość łatwa do zrozumienia, aczkolwiek bardzo żmudna do wykonania w praktyce.

Przykład (przybliżona wartość dla ):${\ displaystyle {\ sqrt {2}}}$

Z i wynika, że leży między 1 a 2. Dlatego próby , itd. Od i widać, że musi być między 1,4 a 1,5. Kontynuacja tej procedury z coraz większą liczbą miejsc dziesiętnych ostatecznie daje przybliżoną wartość z pożądaną dokładnością: ${\ Displaystyle 1 ^ {2} = 1 <2}$${\ Displaystyle 2 ^ {2} = 4> 2}$${\ displaystyle {\ sqrt {2}}}$${\ displaystyle 1 {,} 1 ^ {2}}$${\ displaystyle 1 {,} 2 ^ {2}}$${\ Displaystyle 1 {,} 4 ^ {2} = 1 {,} 96 <2}$${\ displaystyle 1 {,} 5 ^ {2} = 2 {,} 25> 2}$${\ displaystyle {\ sqrt {2}}}$

${\ Displaystyle 1 {,} 41421356 ^ {2} <2 <1 {,} 41421357 ^ {2} \; \ Rightarrow \; {\ sqrt {2}} \ około 1 {,} 41421356}$

Babilońskie wyrywanie korzeni lub metoda czapli

Ta metoda iteracji jest często używana podczas programowania obliczania pierwiastków dla kalkulatorów, ponieważ szybko się zbiega . Jest to metoda Newtona znajdowania zer zastosowanych do funkcji .${\ displaystyle x \ mapsto x ^ {2} -a}$

Rozwój serii Taylor

Rozwinięcie funkcji pierwiastka w szereg Taylora z punktem rozszerzenia może być użyte jako rozwinięcie Taylora wokół punktu jako szereg dwumianowy${\ displaystyle t \ mapsto {\ sqrt {t}}}$${\ displaystyle t = 1}$${\ Displaystyle x \ mapsto (1 + x) ^ {1/2}}$${\ displaystyle x = 0}$

${\ Displaystyle \ sum _ {n = 0} ^ {\ infty} {\ binom {1/2} {n}} \, x ^ {n} = \ sum _ {n = 0} ^ {\ infty} { \ binom {2n} {n}} \, {\ frac {(-1) ^ {n + 1}} {(2n-1) \, 4 ^ {n}}} \, x ^ {n} = 1 + {\ frac {1} {2}} x - {\ frac {1} {8}} x ^ {2} + {\ frac {1} {16}} x ^ {3} - {\ frac {5 } {128}} x ^ {4} \ pm \ dotsb}$

można znaleźć, ponieważ ten szereg jest zbieżny punktowo . Z takimi wynikami ${\ displaystyle | x | \ leq 1}$${\ displaystyle {\ sqrt {1 + x}}}$ ${\ Displaystyle x: = t-1}$

${\ Displaystyle {\ sqrt {t}} = 1 + {\ Frac {1} {2}} (T-1) - {\ Frac {1} {8}} (T-1) ^ {2} + { \ frac {1} {16}} (t-1) ^ {3} - {\ frac {5} {128}} (t-1) ^ {4} \ pm \ dotsb}$ Dla ${\ Displaystyle 0 \ równoważnik t \ równoważnik 2.}$

Obliczenia za pomocą algorytmu CORDIC

Ta metoda jest używana głównie w kalkulatorach, jednostkach FPU i mikrokontrolerach .

Graficzne wyznaczanie pierwiastka kwadratowego

Jedną z możliwości jest Kathetensatz : liczba, której szukany jest pierwiastek kwadratowy, znajduje się na linii liczbowej pokrytej. Na odległości między i ( koło Talesa ) narysowane jest półkole z promieniem . Przy ustalana jest prostopadła do linii bazowej, która przecina półkole (wysokość prawego trójkąta). Odległość od tego punktu przecięcia do punktu zerowego jest pierwiastkiem kwadratowym z (cathetus). ${\ displaystyle n}$${\ displaystyle 0}$${\ displaystyle 0}$${\ displaystyle n}$${\ displaystyle r = {\ tfrac {n} {2}}}$${\ displaystyle 1}$${\ displaystyle n}$

Pierwiastki kwadratowe liczb zespolonych

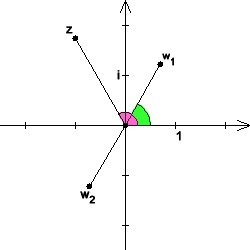
Ekstrakcja korzeni odpowiada dwusieczności kąta w złożonej płaszczyźnie. Przykład:${\ displaystyle {\ sqrt {\ mathrm {i}}}}$

Jeśli liczba zespolona inna niż zero, to równanie ma ${\ displaystyle z}$

${\ Displaystyle w ^ {2} = z}$

dokładnie dwa rozwiązania , znane również jako pierwiastki lub pierwiastki kwadratowe funkcji . Leżą one na płaszczyźnie liczb Gaussa w dwóch punktach przecięcia koła wokół 0 z promieniem i dwusieczną kąta między promieniami wychodzącymi z lub przez . Jeden z dwóch pierwiastków leżących w prawej półpłaszczyźnie nazywany jest główną wartością pierwiastka. Dla ujemnego (rzeczywistego) pierwiastka z dodatnią częścią urojoną jest główną wartością. ${\ displaystyle w}$${\ displaystyle z}$${\ displaystyle {\ sqrt {| z |}}}$${\ displaystyle 0}$${\ displaystyle 1}$${\ displaystyle z}$${\ displaystyle z}$

Jeśli napiszesz liczbę zespoloną w formularzu ${\ displaystyle z}$

${\ displaystyle z = r \ cdot {\ rm {e ^ {\ mathrm {i} \ varphi},}}}$

gdzie i są prawdziwe z i , to do głównej wartości pierwiastka stosuje się następujące zasady: ${\ displaystyle \ varphi}$${\ displaystyle r}$${\ displaystyle r> 0}$${\ Displaystyle - \ pi <\ varphi \ leq \ pi}$

${\ Displaystyle w_ {1} = {\ sqrt {r}} \ cdot {\ rm {e ^ {\ mathrm {i} \ varphi / 2}}}}$

Druga wartość pierwiastka kwadratowego (wartość drugorzędna) wynika z odbicia punktu (obrót o 180 °) w punkcie zerowym:

${\ Displaystyle w_ {2} = {\ sqrt {r}} \ cdot {\ rm {e ^ {\ mathrm {i} (\ varphi / 2 + \ pi)}}}}$

definicja

Złożona funkcja „ kwadrat z ”, podobnie jak rzeczywista funkcja kwadratowa, nie ma funkcji odwrotnej, ponieważ nie jest iniekcyjna , ale w przeciwieństwie do liczb rzeczywistych jest suriektywna, to znaczy każda liczba zespolona jest kwadratem liczby zespolonej. Analogicznie do rzeczywistych (nieujemnych) pierwiastków kwadratowych, można zatem zdefiniować złożone funkcje pierwiastka kwadratowego, ograniczając dziedzinę definicji do podzbioru liczb zespolonych, na których jest iniekcyjny i pozostaje surjektywny. W zależności od wybranego podzbioru otrzymujesz różne gałęzie funkcji pierwiastka kwadratowego jako odwrotność. ${\ Displaystyle q \ colon \ mathbb {C} \ rightarrow \ mathbb {C}; z \ mapsto z ^ {2}}$${\ displaystyle q}$${\ displaystyle D}$${\ displaystyle q}$

Głównej gałęzi złożonej funkcji pierwiastka kwadratowego wyniki, jeśli korzysta się jako domenę${\ displaystyle q}$

${\ Displaystyle D_ {H}: = \ {x + \ mathrm {i} \, y \ in \ mathbb {C} \ mid x> 0 {\ tekst {lub}} (x = 0 {\ tekst {i} } y \ geq 0) \}}$

opiera się na, jest to prawa półpłaszczyzna płaszczyzny liczb zespolonych , gdzie tylko liczby z nieujemną częścią urojoną należą do krawędzi . Ograniczenie to jest bijektywnym odwzorowaniem do na liczby zespolone, więc jego funkcja odwrotna, główna gałąź pierwiastka kwadratowego z do, jest całkowicie zdefiniowana. Wartość tej funkcji odwrotnej nazywana jest główną wartością pierwiastka kwadratowego z . Jeśli chodzi o jakąś konkretną liczbę zespoloną, to jest to ta główna wartość. ${\ displaystyle D_ {H}}$${\ displaystyle q}$${\ displaystyle D_ {H}}$${\ displaystyle D_ {H}}$${\ displaystyle \ mathbb {C}}$${\ displaystyle {\ sqrt {z}}}$${\ displaystyle z}$${\ displaystyle {\ sqrt {z}}}$

Podana jest we współrzędnych kartezjańskich, to znaczy z liczb rzeczywistych i , następnie wyników ${\ displaystyle z}$${\ displaystyle z = x + {\ rm {iy}}}$${\ displaystyle x}$${\ displaystyle y}$

${\ displaystyle {\ sqrt {z}} = {\ sqrt {x + {\ rm {iy}}}} = {\ sqrt {\ tfrac {| z | + x} {2}}} + \ mathrm {i } \ cdot \ operatorname {sgn ^ {+}} (y) \ cdot {\ sqrt {\ tfrac {| z | -x} {2}}}}$

dla głównej wartości pierwiastka kwadratowego, gdzie funkcja ma wartość -1 dla wartości ujemnej, a wartość 1 w innym przypadku (również dla, a zatem różna od funkcji znaku ): ${\ displaystyle \ operatorname {sgn ^ {+}}}$${\ displaystyle y}$${\ displaystyle y = 0}$ ${\ displaystyle \ operatorname {sgn}}$

${\ displaystyle {\ text {sgn}} ^ {+} (y) = {\ początek {przypadków} +1 i {\ tekst {za}} y \ geq 0 \\ - 1 i {\ tekst {za}} y <0 \ end {cases}}}$

Jedyną boczną gałęzią jest${\ displaystyle q}$${\ displaystyle - {\ sqrt {z}}.}$

Jest we współrzędnych biegunowych podanych za pomocą , główna wartość pierwiastka kwadratowego z ${\ displaystyle z}$${\ displaystyle z = | z | \ cdot \ mathrm {e} ^ {\ mathrm {i} \ cdot \ arg (z)}}$${\ Displaystyle \ arg (z) \ in (- \ pi, \ pi]}$

${\ Displaystyle {\ sqrt {z}} = {\ sqrt {| z |}} \ mathrm {e} ^ {\ mathrm {i} \ cdot \ arg (z) / 2}}$

gdzie jest rzeczywisty (nieujemny) pierwiastek kwadratowy z . Drugorzędna wartość ponownie pojawia się jako . ${\ displaystyle {\ sqrt {| z |}}}$${\ displaystyle | z |}$${\ Displaystyle - {\ sqrt {z}} = {\ sqrt {| z |}} \ mathrm {e} ^ {\ mathrm {i} \ cdot (\ arg (z) / 2 + \ pi)}}$

Wielkość dwóch pierwiastków jest zatem pierwiastkiem wartości bezwzględnej liczby zespolonej. W przypadku głównej wartości argument („kąt z ”, patrz poniżej) jest zmniejszony o połowę. Drugie rozwiązanie wynika z geometrycznego odbicia tej głównej wartości na początku . ${\ Displaystyle \ arg (z)}$

Argumentem liczby zespolonej jest zorientowany kąt na płaszczyźnie liczby zespolonej, czyli punkty i współrzędne rzeczywiste. W poniższym przykładzie argument i argument funkcji są wyróżnione kolorem. ${\ displaystyle z = x + \ mathrm {i} \, y}$${\ Displaystyle \ kąt (EOZ)}$${\ Displaystyle E (1 | 0),}$ ${\ Displaystyle O (0 | 0)}$${\ Displaystyle Z (x | y)}$${\ displaystyle z}$${\ displaystyle w_ {1}}$

• Złożony pierwiastek kwadratowy
• 

  Gałąź pierwiastka kwadratowego

• 

  Druga gałąź

• 

  Riemann powierzchni kwadratowych pokazy korzeniowych jak dwie gałęzie łączą.

Przykład: Obliczanie złożonego pierwiastka kwadratowego

Znajdź pierwiastki kwadratowe z Pierwszego, określa się ilość radicand: ${\ displaystyle z = -1 + \ mathrm {i} \, {\ sqrt {3}}.}$

${\ displaystyle | z | = \ lewo | -1+ \ mathrm {i} {\ sqrt {3}} \ prawo | = {\ sqrt {(-1) ^ {2} + ({\ sqrt {3}}) ) ^ {2}}} = {\ sqrt {1 + 3}} = {\ sqrt {4}} = 2}$

Daje to główną wartość pierwiastka kwadratowego do

${\ Displaystyle {\ rozpocząć {wyrównane} w_ {1} & = {\ sqrt {\ tfrac {2 + (- 1)} {2}}} + \ mathrm {i} \ cdot \ operatorname {sgn ^ {+} } ({\ sqrt {3}}) \ cdot {\ sqrt {\ tfrac {2 - (- 1)} {2}}} \\ [0.3em] & = {\ sqrt {\ tfrac {1} {2 }}} + \ mathrm {i} \ cdot (+1) \ cdot {\ sqrt {\ tfrac {3} {2}}} = {\ sqrt {2}} \ cdot \ left ({\ tfrac {1} {2}} + \ mathrm {i} \ cdot {\ tfrac {1} {2}} {\ sqrt {3}} \ right) \ end {aligned}}}$

Drugi korzeń uzyskuje się poprzez odwrócenie znaku:

${\ Displaystyle w_ {2} = - w_ {1} = {\ sqrt {2}} \ cdot \ left (- {\ tfrac {1} {2}} - \ mathrm {i} \ cdot {\ tfrac {1 } {2}} {\ sqrt {3}} \ right)}$

Prawo energetyczne

Prawo władzy

${\ Displaystyle (a \ cdot b) ^ {r} = a ^ {r} \ cdot b ^ {r} \ qquad \ qquad \ qquad \ qquad \ qquad \ qquad \ quad {\ tekst {(P)}}}$

nie nie stosuje się do każdego , nawet do głównych wartości korzeni. Widać to już w szczególnym przypadku wynikającym z dalszej specyfikacji${\ displaystyle r = 1/2}$ ${\ displaystyle a, b \ in \ mathbb {C}}$
${\ Displaystyle a = b =: z}$

${\ displaystyle {\ sqrt {z ^ {2}}} = \ lewo ({\ sqrt {z}} \ prawej) ^ {2},}$

którzy z powodu tożsamości zbyt ${\ Displaystyle \ lewo ({\ sqrt {z}} \ prawej) ^ {2} = z}$

${\ displaystyle {\ sqrt {z ^ {2}}} = z}$

można uprościć, co najwyraźniej już jakakolwiek liczba ujemna daje kontrprzykład dotyczący : ${\ displaystyle z = -1}$

Z powodu i główna wartość argumentu ma argument , podczas gdy wartość główna argumentu ma argument .${\ Displaystyle (-1) ^ {2} = 1}$${\ Displaystyle \ arg (1) = 0}$${\ Displaystyle {\ sqrt {(-1) ^ {2}}}}$${\ Displaystyle \ arg ({\ sqrt {1}}) = 0/2 = 0}$${\ displaystyle -1}$${\ Displaystyle \ arg (-1) = \ pi}$

Uwagi

1. Ponieważ podstawowe wartości pierwiastków z dodatnich radicandów muszą być dodatnie, kontrprzykład pokazuje, że nie może istnieć funkcja pierwiastka kwadratowego, dla której prawo potęgowe ma zastosowanie do wszystkich .${\ displaystyle {\ text {(P)}}}$${\ displaystyle a, b \ in \ mathbb {C}}$
2. Dla i każdy jeden może swobodnie wybrać „znak” dwóch z trzech korzeni, po czym dokładnie jeden pozostaje możliwość na „znak” w ostatnim trymestrze.${\ displaystyle r = 1/2}$${\ displaystyle a, b \ in \ mathbb {C}}$${\ displaystyle {\ text {(P)}}}$

Pierwiastki kwadratowe modulo n

Pierwiastki kwadratowe można również zdefiniować w pierścieniu pozostałych klas . Analogicznie do liczb rzeczywistych i zespolonych pierwiastek kwadratowy nazywamy, jeśli: ${\ Displaystyle \ mathbb {Z} / n \ mathbb {Z}}$${\ displaystyle q}$${\ displaystyle x}$

${\ Displaystyle q ^ {2} \ equiv x {\ bmod {n}}}$

Jednak do obliczenia pierwiastków kwadratowych modulo należy zastosować inne metody niż do obliczenia rzeczywistych lub złożonych pierwiastków kwadratowych. Aby znaleźć pierwiastki kwadratowe z modulo , można postępować w następujący sposób: ${\ displaystyle n}$${\ displaystyle x}$${\ displaystyle n}$

Najpierw określ czynniki pierwsze

${\ Displaystyle n = p_ {1} ^ {m_ {1}} \ cdot p_ {2} ^ {m_ {2}} \ dotsm p_ {k} ^ {m_ {k}}}$

modułu, a następnie rozwiązania modulo poszczególnych mocarstw głównych . Te rozwiązania są ostatecznie zestawiane z wykorzystaniem chińskiej pozostałej części prawa, aby stworzyć rozwiązanie, którego szukasz . ${\ displaystyle n}$${\ displaystyle p ^ {m.}}$

Obliczanie pierwiastków kwadratowych modulo liczba pierwsza p

Przypadek jest prosty: z powodu i modulo 2 każda liczba ma jednoznacznie określony pierwiastek kwadratowy, a mianowicie samą siebie. Dla liczb pierwszych nie równych 2 obliczenia pierwiastków kwadratowych wykonuje się w następujący sposób: ${\ displaystyle p = 2}$${\ Displaystyle 0 ^ {2} = 0, \, 1 ^ {2} = 1}$${\ displaystyle 1 \ not \ equiv 0 {\ bmod {2}}}$ ${\ displaystyle p}$${\ displaystyle x}$

Aby sprawdzić, czy ma nawet pierwiastek kwadratowy w , obliczamy wartość symbolu Legendre${\ displaystyle x}$${\ Displaystyle \ mathbb {Z} / p \ mathbb {Z}}$

${\ Displaystyle \ lewo ({\ Frac {x} {p}} \ prawej) \ equiv x ^ {\ Frac {p-1} {2}} {\ bmod {p}}}$,

ponieważ dotyczy:

${\ Displaystyle \ lewo ({\ Frac {x} {p}} \ prawej) = {\ rozpocząć {przypadków} -1, & {\ tekst {if}} x {\ tekst {moduł kwadratowy nie pozostały}} p {\ text {is}} \\ 0, & {\ text {if}} x {\ text {and}} p {\ text {nie są liczbą pierwszą}} \\ 1, & {\ text {if}} x {\ text {a kwadratowa reszta modulo}} p {\ text {is}} \ end {przypadki}}}$

W pierwszym przypadku nie ma pierwiastka kwadratowego, aw drugim ma on tylko pierwiastek kwadratowy 0. Ciekawym przypadkiem jest zatem trzeci przypadek, a zatem zakładamy w dalszej części, że tak jest. ${\ displaystyle x}$${\ Displaystyle \ mathbb {Z} / p \ mathbb {Z}}$${\ Displaystyle {\ bigl (} {\ tfrac {x} {p}} {\ bigr)} = 1}$

Obliczenie dla przypadku p mod 4 = 3

Jeśli symbol Legendre jest równy 1, to są ${\ displaystyle {\ bigl (} {\ tfrac {x} {p}} {\ bigr)}}$

${\ displaystyle q \ equiv \ pm x ^ {\ frac {p + 1} {4}} {\ bmod {p}}}$

dwa pierwiastki kwadratowe z modulo . ${\ displaystyle x}$${\ displaystyle p}$

Obliczenie dla przypadku p mod 4 = 1

Jeśli symbol Legendre jest równy 1, to są ${\ displaystyle {\ bigl (} {\ tfrac {x} {p}} {\ bigr)}}$

${\ Displaystyle q \ equiv \ pm {\ Frac {x} {2r}} \ lewo (W _ {\ Frac {p-1} {4}} + W _ {\ Frac {p + 3} {4}} \ right) {\ bmod {p}}}$

dwa pierwiastki kwadratowe z modulo . Tutaj tak wybierasz${\ displaystyle x}$${\ displaystyle p}$${\ displaystyle r}$

${\ Displaystyle \ lewo ({\ Frac {r ^ {2} -4x} {p}} \ prawej) = - 1}$

ma zastosowanie. Aby to zrobić, możesz po prostu przetestować różne wartości . Konsekwencja jest rekurencyjna ${\ displaystyle r}$${\ displaystyle W_ {n}}$

${\ Displaystyle W_ {n} = {\ rozpocząć {przypadków} r ^ {2} / x-2, & {\ tekst {if}} n = 1 \\ W_ {n / 2} ^ {2} -2, & {\ text {if}} n {\ text {parzyste}} \\ W _ {(n + 1) / 2} W _ {(n-1) / 2} -W_ {1}, & {\ text {if}} n> 1 {\ text {nieparzyste}} \ end {sprawy}}}$

Są określone.

Przykładowe obliczenia dla i : ${\ displaystyle x = 3}$${\ displaystyle p = 37}$

Zgodnie z powyższym wzorem pierwiastki kwadratowe z ciągu to ${\ displaystyle x}$

${\ Displaystyle q \ equiv \ pm {\ Frac {x} {2r}} \ lewo (W_ {9} + W_ {10} \ po prawej) {\ bmod {3}} 7}$

dany. Ponieważ można znaleźć wartość, próbując , ponieważ obowiązuje: ${\ displaystyle r}$${\ displaystyle r = 2}$

${\ Displaystyle \ lewo ({\ Frac {r ^ {2} -4x} {p}} \ prawej) \ equiv (r ^ {2} -4x) ^ {\ Frac {p-1} {2}} \ equiv (-8) ^ {18} \ equiv 36 \ equiv -1 {\ bmod {3}} 7}$

Wartości i wynikają w następujący sposób: ${\ displaystyle W_ {9}}$${\ displaystyle W_ {10}}$

${\ Displaystyle {\ rozpocząć {matrix} W_ {1} i \ equiv & r ^ {2} / x-2 i \ equiv i 4 / 3-2 i \ equiv i 24 i {\ bmod {3}} 7 \ \ W_ {2} & \ equiv & W_ {1} ^ {2} -2 & \ equiv & 24 ^ {2} -2 & \ equiv & 19 & {\ bmod {3}} 7 \\ W_ {3} & \ equiv & W_ {1} W_ {2} - W_ {1} & \ equiv & 24 \ cdot 19-24 & \ equiv & 25 & {\ bmod {3}} 7 \\ W_ {4} & \ equiv & W_ {2} ^ {2} -2 & \ equiv & 19 ^ {2} -2 & \ equiv & 26 & {\ bmod {3}} 7 \\ W_ {5} & \ equiv & W_ {2} W_ {3} -W_ {1} & \ equiv & 19 \ cdot 25-24 & \ equiv & 7 & {\ bmod {3}} 7 \\ W_ {9} & \ equiv & W_ {4} W_ {5 } -W_ {1} & \ equiv & 26 \ cdot 7-24 & \ equiv & 10 & {\ bmod {3}} 7 \\ W_ {10} & \ equiv & W_ {5} ^ {2} -2 & \ equiv & 7 ^ {2} -2 & \ equiv & 10 & {\ bmod {3}} 7 \\\ end {matrix}}}$

Podstawienie tych wartości daje

${\ Displaystyle q \ equiv \ pm {\ Frac {x} {2r}} \ lewo (W_ {9} + W_ {10} \ po prawej) \ equiv \ pm {\ Frac {3} {4}} (10+ 10) \ equiv \ pm 15 {\ bmod {3}} 7.}$

To znaczy: 15 i 22 to dwa pierwiastki kwadratowe z 3 modulo 37.

Pierwiastki kwadratowe z macierzy

Pierwiastek z macierzy kwadratowej to wszystkie macierze, które po pomnożeniu przez siebie dają: ${\ displaystyle A}$${\ displaystyle B}$${\ displaystyle A}$

${\ displaystyle A = B \ cdot B \ Leftrightarrow B {\ text {jest rdzeniem}} A}$

Podobnie jak w przypadku pierwiastka kwadratowego z liczb rzeczywistych lub zespolonych, pierwiastek kwadratowy z macierzy niekoniecznie jest unikalny. Jeśli jednak spojrzeć tylko na dodatnio określone macierze symetryczne , to tworzenie pierwiastków jest jednoznaczne: każda pozytywnie określona symetryczna macierz ma jednoznacznie określony pozytywnie określony pierwiastek symetryczny, który uzyskuje się poprzez diagonalizację za pomocą macierzy ortogonalnej ( jest to zawsze możliwe zgodnie z twierdzeniem spektralnym ), a następnie zastąpiono pierwiastki diagonalne ich pierwiastkami; jednak zawsze należy wybierać pozytywny korzeń. Zobacz także rozkład Choleskiego . Wyjątkowość wynika z faktu, że wykładnicza odwzorowania jest dyfeomorfizmu z przestrzeni wektorowej symetrycznych macierzy do podzestawu dodatnio określonych matryc symetrycznych. ${\ displaystyle A}$${\ Displaystyle A ^ {\ Frac {1} {2}}.}$${\ displaystyle A}$

Pierwiastek kwadratowy z przybliżonego operatora całkowego

Można liczbowo przybliżyć określoną funkcję całkową od 0 do z i daną funkcję , która przyjmuje wartości w równoodległych punktach interpolacji , jako mnożenie macierzy w następujący sposób (dla ): ${\ Displaystyle G, \, g_ {i}: = g (x_ {i})}$${\ displaystyle x_ {i}}$${\ displaystyle x_ {i} = ja \ delta x}$${\ Displaystyle i = 0,1, \ dotsc, n-1}$${\ displaystyle F, \, f_ {i}: = f (x_ {i})}$${\ displaystyle x_ {i}}$${\ displaystyle f_ {i}}$ ${\ displaystyle G = FI}$${\ displaystyle n = 4}$

${\ displaystyle G = FI = {\ początek {pmatrix} g_ {0} i g_ {1} i g_ {2} i g_ {3} \\ 0 i g_ {0} i g_ {1} i g_ {2} \\ 0 & 0 & g_ {0} & g_ {1} \\ 0 & 0 & 0 & g_ {0} \ end {pmatrix}} = {\ begin {pmatrix} f_ {0} & f_ {1} & f_ {2} & f_ {3} \\ 0 & f_ {0} & f_ {1} & f_ {2} \\ 0 & 0 & f_ {0} & f_ {1} \\ 0 & 0 & 0 & f_ {0} \ end {pmatrix}} {\ begin {pmatrix} \ Delta x & \ Delta x & \ Delta x & \ Delta x \\ 0 & \ Delta x & \ Delta x & \ Delta x \\ 0 & 0 & \ Delta x & \ Delta x \\ 0 & 0 & 0 & \ Delta x \ end {pmatrix}}}$

Widać wyraźnie, że można powtórzyć tę operację i w ten sposób otrzymać całkę podwójną : ${\ Displaystyle H, \, h_ {i}: = h (x_ {i})}$

${\ displaystyle H = GI = FII = FI ^ {2}}$

Można więc rozumieć macierz jako liczbowo przybliżony operator całkowy. ${\ displaystyle I}$

Macierz nie może być przekątna, a jej jordańska postać normalna to: ${\ displaystyle I}$

${\ Displaystyle {\ rozpocząć {pmatrix} \ Delta x i 1 i 0 i 0 \\ 0 i \ Delta x i 1 i 0 \\ 0 i 0 i \ Delta x i 1 \\ 0 i 0 i 0 i \ Delta x \ end {pmatrix}}}$

Aby wyodrębnić z niego pierwiastek kwadratowy, można postępować zgodnie z opisem dla macierzy, które nie są diagonalizowalne. W tym przypadku istnieje jednak bardziej bezpośrednie rozwiązanie formalne:

${\ Displaystyle I ^ {\ beta} = {\ rozpocząć {pmatrix} \ alfa _ {0} i \ alfa _ {1} i \ alfa _ {2} i \ alfa _ {3} \\ 0 i \ alfa _ {0} & \ alpha _ {1} & \ alpha _ {2} \\ 0 & 0 & \ alpha _ {0} & \ alpha _ {1} \\ 0 & 0 & 0 & 0 & \ alpha _ {0} \ end {pmatrix}}}$

z , i . ${\ Displaystyle \ alfa _ {0} = (\ Delta x) ^ {\ beta}}$${\ Displaystyle \ alfa _ {k} = \ suma _ {j = 1} ^ {k} {\ Frac {\ Gamma (\ beta +1) (- 1) ^ {j + 1} \ alfa _ {kj} } {\ Gamma (j + 1) \ Gamma (\ beta -j + 1)}}}$${\ Displaystyle k = 1,2, \ dotsc, n-1}$

Indeksy oznaczają sub-przekątne (0 to przekątna), a wykładnik jest równy . Jeśli przyjmiemy, że jest prawdziwe i pozytywne, to prawdziwe iz definicji jest pozytywne. ${\ displaystyle \ alpha}$${\ displaystyle \ beta}$${\ displaystyle {\ tfrac {1} {2}}}$${\ displaystyle \ Delta x}$${\ Displaystyle (\ Delta x) ^ {\ Frac {1} {2}}}$

Dzięki temu można liczbowo przybliżyć „połówkową” całkę oznaczoną od 0 do funkcji w następujący sposób: ${\ Displaystyle L, \, l_ {i}: = l (x_ {i})}$${\ displaystyle x_ {i}}$${\ displaystyle f (x)}$

${\ Displaystyle L = FI ^ {\ beta} = {\ rozpocząć {pmatrix} l_ {0} i l_ {1} i l_ {2} i l_ {3} \\ 0 i l_ {0} i l_ {1} & l_ {2} \\ 0 & 0 & l_ {0} & l_ {1} \\ 0 & 0 & 0 & l_ {0} \ end {pmatrix}} = {\ begin {pmatrix} f_ {0} & f_ {1} & f_ {2} & f_ {3} \\ 0 & f_ {0} & f_ {1} & f_ {2} \\ 0 & 0 & f_ {0} & f_ {1} \\ 0 & 0 & 0 & f_ {0} \ end {pmatrix}} {\ begin {pmatrix} \ alpha _ {0} & \ alpha _ {1} & \ alpha _ {2} & \ alpha _ {3} \\ 0 & \ alpha _ {0} & \ alpha _ {1} & \ alpha _ {2} \\ 0 & 0 & \ alpha _ {0} & \ alpha _ {1} \\ 0 & 0 & 0 & \ alfa _ {0} \ end {pmatrix}}}$

Jeśli szukasz wszystkich operatorów, które po pomnożeniu przez siebie dają w wyniku przybliżony operator całkowy , musisz również wstawić znak ujemny, to znaczy istnieją dwa rozwiązania . ${\ displaystyle I}$${\ displaystyle \ pm ja ^ {\ frac {1} {2}}}$

Aby wyprowadzić wzór, możesz najpierw odwrócić, podnieść wynik do potęgi, a następnie ponownie go odwrócić. ${\ displaystyle I}$${\ displaystyle \ beta}$

Zobacz też

• Root of 2 , Euclid's dowód irracjonalności korzenia 2
• Korzeń 3
• Root (matematyka)
• Modulo , szczątkowy pierścień klasy
• Prawo pierwiastków kwadratowych Penrose'a

linki internetowe

Wikisłownik: pierwiastek kwadratowy  - wyjaśnienia znaczeń, pochodzenie słów, synonimy, tłumaczenia

dokumentów potwierdzających

1. ↑ Aktualność prawa potęgowego dla pierwiastków kwadratowych nie będzie, ale zakłada się w cytowanym fragmencie sporadycznie w literaturze (dla ujemnego rzeczywistego pierwiastka sześciennego): Klaus Fritzsche: Samouczek matematyki dla początkujących . Springer-Verlag, 2016, ISBN 978-3-662-48910-9 ( ograniczony podgląd w Google Book Search [dostęp: 4 lipca 2017 r.]).${\ displaystyle {\ text {(P)}}}$