trygonometria

Ilustracje trygonometrii w księdze z 1687 r.

Trygonometria ( grecki τρίγωνον trigonon , Trójkąt i μέτρον Metron , środek „) jest gałęzią geometrii a więc matematyka . Jeśli chodzi o zagadnienia geometrii płaskiej ( planimetrii ) traktowane są trygonometrycznie, mówi się o trygonometrii płaskiej ; istnieje również trygonometria sferyczna , która zajmuje się trójkątami sferycznymi (trójkąty sferyczne) oraz trygonometria hiperboliczna . Poniższe stwierdzenia odnoszą się zasadniczo do dziedziny trygonometrii płaskiej.

Trygonometria bada relacje między bokami i kątami trójkątów. Znając i stosując te zależności (wzory), podane rozmiary trójkąta (długości boków, rozmiary kątów , długości poprzeczek trójkąta itp.), można obliczyć inne brakujące rozmiary trójkąta . Funkcje trygonometryczne ( funkcje trygonometryczne, funkcje kołowe, funkcje goniometryczne) sinus (sin), cos (cos) , tangens (tan), cotangens (cot) , sieczna (sec) i cosecans (csc) są używane jako pomoce . Obliczenia trygonometryczne mogą również odnosić się do bardziej skomplikowanych obiektów geometrycznych, na przykład do wielokątów (wielokątów) , do problemów stereometrii (geometria przestrzenna) oraz do pytań z wielu innych dziedzin (patrz poniżej).

Trygonometria w prawym trójkącie

Trójkąt prostokątny

Szczególnie prosta jest trygonometria trójkąta prostokątnego . Ponieważ suma kątów trójkąta wynosi 180 °, kąt prosty takiego trójkąta jest największym kątem wewnętrznym . Najdłuższy bok (zwany przeciwprostokątną ) jest przeciwny. Dwa krótsze boki trójkąta nazywane są katetami . Odnosząc się do jednego z dwóch mniejszych kątów, warto rozróżnić stronę przeciwną (podany kąt względem) i stronę sąsiednią (przyległą do danego kąta). Teraz definiuje się:

${\ displaystyle {\ zacząć {wyrównany} {\ tekst {Sinus}} \ alfa & = \ grzech \ alfa = {\ frac {a} {c}} = {\ frac {\ tekst {przeciwny katet}} {\ tekst {Hypotenuse}}} \\ [0,5ex] {\ text {cosinus}} \ alfa & = \ cos \ alfa = {\ frac {b} {c}} = {\ frac {\ text {sąsiadujący}} { \ text {Hypotenuse}}} \\ [0,5ex] {\ text {Styczna}} \ alfa & = \ tan \ alfa = {\ frac {a} {b}} = {\ frac {\ text {naprzeciwko cathet} } {\ text {sąsiadujący}}} \\ [0,5ex] {\ text {cotangens}} \ alpha & = \ cot \ alpha = {\ frac {b} {a}} = {\ frac {\ tekst { Sąsiadujący}} {\ tekst {Naprzeciwko}}} \\ [0,5ex] {\ text {Sekans z}} \ alfa & = \ sec \ alpha = {\ frac {c} {b}} = {\ frac {\ text {Hypotenuse}} {\ text {Ankathete}}} \\ [0.5ex] {\ text {Kosekans von}} \ alpha & = \ csc \ alpha = {\ frac {c} {a}} = { \ Frac {\ text {Hypotenuse}} {\ text {Cathet przeciwny}}} \ end {wyrównany}}}$

Definicje te mają sens, ponieważ różne trójkąty prostokątne o danym kącie są do siebie podobne, więc pasują do siebie w swoich proporcjach. Na przykład jeden trójkąt może mieć boki dwa razy dłuższe od drugiego. Do frakcji powyższych równań definicja ma takie same znaczenia w tym przypadku. Czyli te wartości zależą tylko od podanego kąta. Z tego powodu sensowne jest mówienie o funkcjach kątów.

Przykład: Obliczanie długości boku

Poniższe wartości liczbowe są zaokrąglane. W trójkącie ABC podane są następujące wielkości:

${\ displaystyle b = 5 {,} 5 \, {\ mbox {cm}}; \ quad \ alfa = 29 ^ {\ circ}; \ quad \ gamma = 90 ^ {\ circ}}$

Na podstawie tych informacji należy określić długość boku c. Ponieważ sąsiednia strona jest znana i poszukiwana jest przeciwprostokątna, używana jest funkcja cosinus. ${\ styl wyświetlania \ alfa}$

${\ displaystyle \ cos \ alfa = {\ frac {b} {c}}}$

${\ displaystyle c = {\ frac {b} {\ cos \ alfa}} = {\ frac {5 {,} 5 \, {\ mbox {cm}}} {\ cos 29 ^ {\ circ}}} = 6 {,} 3 \, {\ mbox {cm}}}$

Przykład: Obliczanie rozmiaru kąta

Wiadomo o trójkącie ABC:

${\ displaystyle a = 3 {,} 1 \, {\ mbox {cm}}; \ quad b = 5 {,} 5 \, {\ mbox {cm}}; \ quad \ gamma = 90 ^ {\ circ} }$

Poszukiwany jest kąt . Dwie podane strony i są sąsiednimi i przeciwległymi stronami . Dlatego sensowne jest użycie funkcji stycznej. ${\ styl wyświetlania \ beta}$${\ styl wyświetlania a}$${\ styl wyświetlania b}$${\ styl wyświetlania \ beta}$

${\ displaystyle \ tan \ beta = {\ frac {b} {a}} = {\ frac {5 {,} 5 \, {\ mbox {cm}}} {3 {,} 1 \, {\ mbox { cm}}}} = 1 {,} 8}$

Podczas gdy w ostatnim przykładzie wartość cosinusa musiała zostać obliczona dla znanego kąta, tutaj sytuacja jest odwrotna. Przynależny kąt należy określić na podstawie znanej wartości stycznej. Potrzebna jest funkcja odwrotna funkcji stycznej, tzw. funkcja arctangens (arctan) lub zestaw tabel, z których można odczytać kąt i związaną z nim wartość tangensa. To daje:

${\ displaystyle \ beta = 61 {,} 0 ^ {\ circ}}$

Definicja funkcji trygonometrycznych na okręgu jednostkowym

Koło jednostkowe

Wszystkie funkcje trygonometryczne kąta θ można konstruować geometrycznie w okręgu jednostkowym o środku O.

Stosowane do tej pory definicje mogą być stosowane tylko dla kątów poniżej 90 °. Do wielu celów interesują jednak wartości trygonometryczne większych kątów. Koło jednostka , to jest koło o promieniu 1, pozwala na takie rozszerzenie poprzedniej definicji. Dla danego kąta wyznaczany jest odpowiedni punkt na okręgu jednostkowym. Współrzędną x tym punkcie wartość cosinus zadanym kątem, współrzędna y jest wartością sinusoidalnego.

Podaną powyżej definicję wartości sinus i cosinus za pomocą współrzędnych x i y można łatwo rozszerzyć do kątów powyżej 90 °. Można zauważyć, że dla kątów między 90 ° a 270 ° współrzędna x, a tym samym także cosinus, jest ujemna, odpowiednio dla kątów między 180 ° a 360 ° współrzędna y, a zatem również sinus. Definicję można również łatwo przenieść na kąty większe niż 360 ° i kąty ujemne.

Zauważ, że w nowoczesnym podejściu do zdefiniowania kąta używa się relacji między kątem a sinusem lub cosinusem. Same funkcje sinus i cosinus są wprowadzane poprzez ich przedstawienie szeregowe .

Pozostałe cztery funkcje trygonometryczne są zdefiniowane przez:

${\ displaystyle \ tan \ alfa = {\ frac {\ grzech \ alfa} {\ cos \ alfa}}}$

${\ displaystyle \ cot \ alfa = {\ frac {1} {\ tan \ alfa}} = {\ frac {\ cos \ alfa} {\ grzech \ alfa}}}$

${\ styl wyświetlania \ sek \ alfa = {\ frac {1} {\ cos \ alfa}}}$

${\ displaystyle \ csc \ alfa = {\ frac {1} {\ grzech \ alfa}}}$

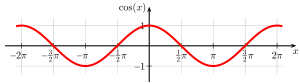
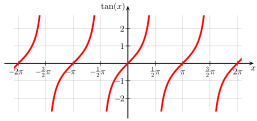
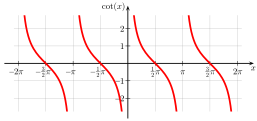
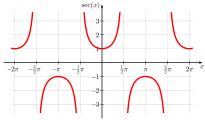
• Wykresy głównych funkcji trygonometrycznych (kąty w radianach, czyli π ≙ 180 °)
• 

  Sinus

• 

  cosinus

• 

  tangens

• 

  cotangens

• 

  Secans

• 

  cosecant

Trygonometria w ogólnym trójkącie

Opracowano również szereg wzorów dla ogólnych trójkątów, które umożliwiają określenie nieznanych długości boków lub rozmiarów kątów. W szczególności należy tu wspomnieć o prawie sinusów i prawie cosinusów . Korzystanie z prawa sinusów

${\ displaystyle {\ frac {a} {\ sin \ alfa}} = {\ frac {b} {\ grzech \ beta}} = {\ frac {c} {\ grzech \ gamma}}}$

jest przydatne, gdy znane są dwa boki i jeden z dwóch przeciwnych kątów lub jeden bok i dwa kąty trójkąta. Prawo cosinusów

${\ displaystyle a ^ {2} \, = \, b ^ {2} + c ^ {2} -2bc \ cos \ alpha}$

${\ displaystyle b ^ {2} \, = \, a ^ {2} + c ^ {2} -2ac \ cos \ beta}$

${\ displaystyle c ^ {2} \, = \, a ^ {2} + b ^ {2} -2ab \ cos \ gamma}$

umożliwia obliczenie kątów z trzech podanych stron lub przeciwnej strony z dwóch stron i ich kąta pośredniego. Kolejne wzory, które mają zastosowanie do każdego trójkąta to twierdzenie styczna The twierdzenie połowa kąta (cotangent tw) i Mollweidian wzory .

Właściwości i formuły

Artykuły dotyczące sześciu funkcji trygonometrycznych ( sinus , cosinus , tangens , cotangens , secans , kosecans ) oraz zbiór formuł trygonometrycznych zawierają liczne właściwości tych funkcji i formuły do ​​ich obliczania. Szczególnie często stosowane są wzory uzupełniające dla sinusa i cosinusa

${\ displaystyle \ grzech (90 ^ {\ circ} - \ alfa) \, = \, \ cos \ alfa}$

${\ displaystyle \ cos (90 ^ {\ circ} - \ alfa) \, = \, \ sin \ alfa}$

a także „ Pitagoras trygonometryczny ”

${\ displaystyle \ sin ^ {2} \ alfa + \ cos ^ {2} \ alfa \, = 1}$

Ważne są również twierdzenia o dodawaniu funkcji trygonometrycznych i wyciągane z nich wnioski. Chodzi o wartości trygonometryczne sum lub różnice kątów. Na przykład dla wszystkich i : ${\ styl wyświetlania \ alfa}$${\ styl wyświetlania \ beta}$

${\ displaystyle \ sin (\ alfa \ pm \ beta) = \ sin \ alfa \ cdot \ cos \ beta \ pm \ cos \ alfa \ cdot \ sin \ beta}$

${\ displaystyle \ cos (\ alfa \ pm \ beta) = \ cos \ alfa \ cdot \ cos \ beta \ mp \ sin \ alfa \ cdot \ sin \ beta}$

${\ displaystyle \ cos \ alfa + \ cos \ beta = 2 \ cos {\ frac {\ alfa + \ beta} {2}} \ cos {\ frac {\ alfa - \ beta} {2}}}$

${\ displaystyle \ cos \ alfa - \ cos \ beta = -2 \ grzech {\ frac {\ alfa + \ beta} {2}} \ grzech {\ frac {\ alfa - \ beta} {2}}}$

${\ displaystyle \ grzech \ alfa + \ grzech \ beta = 2 \ grzech {\ frac {\ alfa + \ beta} {2}} \ cos {\ frac {\ alfa - \ beta} {2}}}$

${\ displaystyle \ sin \ alfa - \ sin \ beta = 2 \ cos {\ frac {\ alfa + \ beta} {2}} \ grzech {\ frac {\ alfa - \ beta} {2}}}$

Dalsze tożsamości można znaleźć w kolekcji formuł trygonometrycznych .

obszary zastosowania

Historyczna ilustracja pomiaru terenu za pomocą trójkąta (1667)

Trygonometria odgrywa kluczową rolę w wielu obszarach:

W geodezji (miernictwie) mówi się o triangulacji, gdy celuje się w inne punkty z punktów o znanej pozycji (pomiar kąta) i wyznacza trygonometrycznie położenia nowych punktów. W astronomii odległości do planet, księżyców i pobliskich gwiazd stałych można określić w odpowiedni sposób. Równie ważne jest znaczenie trygonometrii w nawigacji samolotów i statków oraz w astronomii sferycznej , zwłaszcza przy obliczaniu pozycji gwiazd i planet.

W fizyce funkcje sinusa i cosinusa są używane do matematycznego opisu drgań i fal . To samo dotyczy przebiegu czasowego napięcia elektrycznego i natężenia prądu elektrycznego w technologii prądu przemiennego .

fabuła

Prekursy trygonometrii istniały w matematyce greckiej już w starożytności . Arystarch z Samos wykorzystał właściwości trójkątów prostokątnych do obliczenia relacji odległości między ziemią a słońcem lub księżycem. W astronomowie Hipparch i Ptolemy znane są prace z ścięgien tabelach, to jest z tabel konwersji kąt środkowy (kąt środkowy) do długości pasów dźwigarów kratowych , i vice versa. Wartości takich tabel są bezpośrednio związane z funkcją sinus: Długość cięciwy kołowej wynika z promienia okręgu i kąta środkowego według ${\ styl wyświetlania r}$${\ styl wyświetlania \ alfa}$

${\ displaystyle s = 2r \ grzech {\ frac {\ alfa} {2}}.}$

Podobne tabele były również używane w matematyce indyjskiej . Arabscy naukowcy przejęli wyniki Greków i Hindusów oraz rozszerzyli trygonometrię, zwłaszcza trygonometrię sferyczną. W średniowiecznej Europie znajomość trygonometrii arabskiej była znana dopiero późno. Obszar ten został po raz pierwszy systematycznie wytyczony w XV wieku. W epoce renesansu narastające problemy balistyki i żeglugi morskiej wymagały udoskonalenia trygonometrii i tablicy trygonometrycznej . Niemiecki astronom i matematyk Regiomontanus (Johann Müller) podsumował teorie i metody trygonometrii płaskiej i sferycznej w pięciotomowej pracy De triangulis omnimodis . W związku z tym zastosowaniem oprócz sinusa i cosinusa wykorzystano również inne funkcje trygonometryczne, takie jak sinus versus = 1 - cos.

Termin trygonometria został wprowadzony przez Bartholoma Pitiscusa w jego Trigonometria: sive de solutione triangulorum tractatus brevis et perspicuus z 1595 roku.

Większość notacji używanych dzisiaj i analityczna reprezentacja funkcji trygonometrycznych pochodzi od Leonharda Eulera .

literatura

• Theophil Lambacher, Wilhelm Schweizer (red.): Trygonometria poziomu, praca dydaktyczna dla szkół wyższych. Ernst Klett Verlag, Stuttgart, 1958.
• Heinz Pester, Wolfgang Pauli: Podręcznik i zeszyt do matematyki . Wydanie XXI. Tom II Planimetria, stereometria i trygonometria płaszczyzny . Fachbuchverlag, Lipsk 1991, ISBN 978-3-446-00755-0 . 

linki internetowe

Wikisłownik: Trygonometria  - wyjaśnienia znaczeń, pochodzenie słów, synonimy, tłumaczenia

• Pomoc w trygonometrii Dynamiczne dokumenty do zrozumienia funkcji trygonometrycznych
• Trygonometria podsumowująca dla liceum. Państwowy serwer edukacyjny Badenia-Wirtembergia
• Proste równania trygonometryczne, przykładowe problemy z poradami dotyczącymi rozwiązań. Państwowy serwer edukacyjny Badenia-Wirtembergia
• Trygonometryczne aplety Java
• Trygonometria dla studentów w internetowej książce do matematyki
• O historii trygonometrii
• Funkcje trygonometryczne
• Trygonometria Aplikacja internetowa Obliczenia trygonometryczne w czasie rzeczywistym