Maszyna wektorów nośnych

Maszyny wektorów nośnych [ səpɔːt vektə məʃiːn ] ( SVM , tłumaczenie z angielskiego „ maszyny wektorów nośnych metoda” lub wektorów nośnych nie jest używana) służy jako klasyfikator (patrz klasyfikacja ) i regressor (patrz analizy regresji ). Maszyna wektorów nośnych dzieli wiele obiektów na klasy w taki sposób, że możliwie najszerszy obszar wokół granic klas pozostaje wolny od obiektów; jest to tak zwany klasyfikator dużej marży (ang. „szeroki klasyfikator marży”).

Maszyny wektorów nośnych nie są maszynami w tradycyjnym sensie, tj. Nie składają się z elementów materialnych. Jest to czysto matematyczna metoda rozpoznawania wzorców stosowana w programach komputerowych . W związku z tym część nazwy machine nie odnosi się do maszyny , ale do obszaru pochodzenia maszyn wektora nośnego, uczenia maszynowego .

Podstawowa funkcjonalność

Dwie możliwe linie podziału o różnych rozmiarach krawędzi

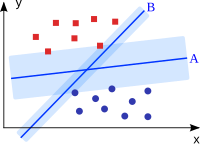
Punktem wyjścia do budowy maszyny wektorów nośnych jest zbiór obiektów szkoleniowych, dla których wiadomo, do jakiej klasy należą. Każdy obiekt jest reprezentowany przez wektor w przestrzeni wektorowej . Zadaniem maszyny wektorów nośnych jest umieszczenie w tej przestrzeni hiperpłaszczyzny , która działa jako powierzchnia oddzielająca i dzieli obiekty szkoleniowe na dwie klasy. Odległość między wektorami, które są najbliżej hiperpłaszczyzny, jest zmaksymalizowana. Ta szeroka, pusta ramka powinna później zapewnić, że obiekty, które nie odpowiadają dokładnie obiektom szkoleniowym, zostaną sklasyfikowane tak niezawodnie, jak to tylko możliwe.

Podczas korzystania z hiperpłaszczyzny nie jest konieczne uwzględnienie wszystkich wektorów uczących. Wektory, które są dalej od hiperpłaszczyzny i są do pewnego stopnia „ukryte” za przednią częścią innych wektorów, nie wpływają na położenie i położenie płaszczyzny podziału. Hiperpłaszczyzna zależy tylko od wektorów najbliższych jej - i tylko one są potrzebne do dokładnego matematycznego opisu płaszczyzny. Wektory te są najbliższe ich funkcyjnym wektorom wspomagającym (ang. Ang. Support wektory ), nazywanym i pomagającym wspierać maszyny wektorowe zgodnie z ich nazwą.

Liniowa rozdzielność

Hiperpłaszczyzna nie może być „wygięta”, tak aby czyste oddzielenie hiperpłaszczyzną było możliwe tylko wtedy, gdy obiekty można rozdzielić liniowo . Ten warunek zwykle nie jest spełniony w przypadku rzeczywistych zestawów obiektów szkoleniowych. W przypadku danych, które można rozdzielić nieliniowo, maszyny obsługujące wektory wykorzystują sztuczkę jądra do rysowania nieliniowej granicy klas.

Idea kryjąca się za sztuczką jądra polega na przeniesieniu przestrzeni wektorowej, a tym samym również wektorów uczących w niej do przestrzeni wyższego wymiaru. W przestrzeni o wystarczająco dużej liczbie wymiarów - w razie wątpliwości nieskończonej - nawet najbardziej zagnieżdżony zbiór wektorów można rozdzielić liniowo. W tej wielowymiarowej przestrzeni oddzielająca hiperpłaszczyzna jest teraz określona. Podczas odwrotnej transformacji do przestrzeni o niższych wymiarach, liniowa hiperpłaszczyzna staje się nieliniową, być może nawet nieciągłą hiperpowierzchnią , która starannie oddziela wektory uczące na dwie klasy.

Z tym procesem wiążą się dwa problemy: Wysoka transformacja jest niezwykle ciężka obliczeniowo, a reprezentacja interfejsu w przestrzeni niskowymiarowej jest na ogół niezwykle złożona i dlatego praktycznie nie nadaje się do użytku. Tutaj pojawia się sztuczka jądra. Jeśli ktoś użyje odpowiednich funkcji jądra do opisu interfejsu, które opisują hiperpłaszczyznę w układzie wysokowymiarowym i nadal pozostają „łagodne” w niskowymiarowych, możliwe jest zaimplementowanie transformacji do przodu i do tyłu bez konieczności wykonywania tego arytmetycznie. Tutaj również niektóre wektory są wystarczające, a mianowicie wektory wspomagające, aby w pełni opisać granicę klas.

Zarówno liniowe, jak i nieliniowe maszyny z wektorami nośnymi mogą być projektowane bardziej elastycznie z dodatkowymi zmiennymi poślizgu . Zmienne poślizgu pozwalają klasyfikatorowi na niepoprawną klasyfikację poszczególnych obiektów, ale jednocześnie „karają” każdą taką błędną klasyfikację. W ten sposób z jednej strony unika się nadmiernego dopasowania , az drugiej zmniejsza się wymagana liczba wektorów nośnych.

Implementacja matematyczna

SVM określa na podstawie zestawu przykładów szkoleniowych

${\ Displaystyle \ {(\ mathbf {x} _ {i}, y_ {i}) \ mid ja = 1, \ dotsc, m; \ y_ {i} \ in \ {- 1,1 \} \}}$

hiperpłaszczyzna który oddziela dwie klasy tak wyraźnie, jak to możliwe.

Oznacza to wyraźnie, co następuje: Wektor normalny  opisuje linię prostą przechodzącą przez początek współrzędnych. Hiperpłaszczyzny biegną prostopadle do tej prostej. Każdy przecina linię w pewnej odległości od początku (mierzonej w kierunku przeciwnym do ). Ta odległość nazywana jest odchyleniem . Razem wektor normalny i odchylenie jasno definiują hiperpłaszczyznę, a do punktów do niej należą : ${\ displaystyle \ mathbf {w}}$${\ Displaystyle {\ tfrac {b} {\ | \ mathbf {w} \ | _ {2}}}}$${\ displaystyle \ mathbf {w}}$${\ displaystyle \ mathbf {x}}$

${\ displaystyle \ langle \ mathbf {w}, \ mathbf {x} \ rangle + b = 0}$.

W przypadku punktów, które nie znajdują się na hiperpłaszczyźnie, wartość nie jest zerowa, ale dodatnia (po wskazanej stronie ) lub ujemna (po drugiej stronie). Znaku można użyć do nazwania strony, po której leży punkt. ${\ displaystyle \ mathbf {w}}$

Jeśli hiperpłaszczyzna oddziela dwie klasy, to znak jest dodatni dla wszystkich punktów w jednej klasie i ujemny dla wszystkich punktów w drugiej klasie. Teraz celem jest znalezienie takiej hiperpłaszczyzny.

Jeśli ktoś wyrazi przynależność do klasy w przykładach szkoleniowych , to skutkuje to formułowym warunkiem ${\ displaystyle y_ {i} = \ pm 1}$

${\ displaystyle y_ {i} = \ operatorname {sgn} (\ langle \ mathbf {w}, \ mathbf {x} _ {i} \ rangle + b)}$

Jeśli taka hiperpłaszczyzna w ogóle istnieje, to jest nieskończenie wiele, które różnią się tylko minimalnie, a czasami są bardzo zbliżone do jednej lub drugiej klasy. Istnieje jednak ryzyko, że punkty danych, które napotkamy w przyszłości, będą znajdować się po „złej” stronie hiperpłaszczyzny, a tym samym zostaną źle zinterpretowane.

Hiperpłaszczyzna powinna zatem być taka, aby najmniejsza odległość punktów szkoleniowych do hiperpłaszczyzny, tzw. Margines (od angielskiego marginesu , marginesu), była zmaksymalizowana, aby zapewnić jak najlepsze uogólnienie do klasyfikatora.

Celem tzw. Treningu jest obliczenie parametrów i tej „najlepszej” hiperpłatności. ${\ displaystyle \ mathbf {w}}$${\ displaystyle b}$

Hiperpłaszczyzna jest następnie używana jako funkcja decyzyjna . Oznacza to: zakłada się, że obliczony znak będzie również poprawnie odzwierciedlał przynależność do klasy dla przyszłych punktów danych. W szczególności komputer może łatwo i automatycznie przeprowadzić klasyfikację, po prostu obliczając znak.

Dane rozdzielne liniowe

Wiele algorytmów uczących się działa z hiperpłaszczyzną, którą można przedstawić w kategoriach dwuwymiarowych za pomocą funkcji liniowej . Czy dwie klasy przykładów można oddzielić od siebie hiperpłaszczyzną, tj. H. jednak możliwe do rozdzielenia liniowego , zwykle istnieje nieskończona liczba hiperpłaszczyzn, które oddzielają od siebie te dwie klasy. SVM różni się od innych algorytmów uczących się tym, że wybiera ten z minimalną normą kwadratową ze wszystkich możliwych oddzielających hiperpłaszczyzn , tak że to samo dotyczy każdego przykładu szkoleniowego . Odpowiada to maksymalizacji najmniejszej odległości od hiperpłaszczyzny ( marginesu ). Zgodnie z statystyczną teorią uczenia się , złożoność klasy wszystkich hiperpłaszczyzn z pewnym marginesem jest mniejsza niż klasy wszystkich hiperpłaszczyzn z mniejszym marginesem. Na tej podstawie można wyprowadzić górne granice oczekiwanego błędu uogólnienia maszyny SVM. ${\ Displaystyle \ | \ mathbf {w} \ | _ {2} ^ {2}}$${\ Displaystyle y_ {i} (\ langle \ mathbf {w}, \ mathbf {x} _ {i} \ rangle + b) \ geq 1}$${\ displaystyle \ mathbf {x} _ {i}}$

Problem optymalizacji można następnie zapisać jako:

Zminimalizuj termin , dostosowując zmienne ,${\ Displaystyle {\ Frac {1} {2}} \ | \ mathbf {w} \ | _ {2} ^ {2}}$${\ displaystyle \ mathbf {w}, b}$

tak, aby ograniczenie dotyczyło wszystkich .${\ Displaystyle y_ {i} (\ langle \ mathbf {w}, \ mathbf {x} _ {i} \ rangle + b) \ geq 1}$${\ Displaystyle 1 \ równoważnik i \ równoważnik m}$

Dane rozdzielne nieliniowo

Z reguły przykłady szkoleniowe nie mogą być ściśle rozdzielone liniowo. Może to obejmować błędy pomiaru w danych lub fakt, że rozkłady obu klas w naturalny sposób się pokrywają. W tym przypadku problem optymalizacji zmienia się w taki sposób, że możliwe są naruszenia warunków wtórnych, ale naruszenia powinny być jak najmniejsze. W tym celu dla każdego warunku drugorzędnego wprowadzana jest zmienna dodatniego poślizgu , której wartością jest naruszenie warunków wtórnych. oznacza, że ​​został naruszony warunek wtórny. Ponieważ suma naruszeń powinna być jak najmniejsza, suma błędów jest dodawana do funkcji docelowej, a tym samym również minimalizowana. Ponadto suma ta jest mnożona przez dodatnią stałą, która reguluje równowagę między minimalizacją a prawidłową klasyfikacją przykładów szkoleniowych. Problem optymalizacji ma wtedy następującą postać: ${\ displaystyle m}$ ${\ displaystyle \ xi _ {i}}$${\ displaystyle \ xi _ {i}> 0}$${\ displaystyle C}$${\ Displaystyle {\ Frac {1} {2}} \ | \ mathbf {w} \ | _ {2} ^ {2}}$

Zminimalizuj termin , dostosowując zmienne ,${\ Displaystyle {\ Frac {1} {2}} \ | \ mathbf {w} \ | _ {2} ^ {2} + C \ suma _ {i = 1} ^ {m} \ xi _ {i} }$${\ displaystyle \ mathbf {w}, b, \ xi _ {i}}$

tak, aby ograniczenie dotyczyło wszystkich .${\ Displaystyle y_ {i} (\ langle \ mathbf {w, x_ {i}} \ rangle + b) \ geq 1- \ xi _ {i}}$${\ Displaystyle 1 \ równoważnik i \ równoważnik m}$

Podwójny problem

Oba kryteria optymalizacji są wypukłe i można je skutecznie rozwiązać nowoczesnymi metodami. Ta prosta optymalizacja i właściwość obsługująca maszyny wektorowe w dużej mierze pozwalają uniknąć nadmiernego dopasowania do danych testowych użytych do zaprojektowania klasyfikatora, sprawiły, że metoda ta jest niezwykle popularna i szeroko stosowana.

Przykład klasyfikacji z SVM. W holu widać oddzielającą hiperpłaszczyznę (czarna linia) i wektory pomocnicze (zakreślone cienkim turkusem).

Opisany powyżej problem optymalizacji jest zwykle rozwiązywany w dwojakiej formie. To sformułowanie jest równoważne z pierwotnym problemem w tym sensie, że wszystkie rozwiązania dualności są również rozwiązaniami pierwotnego problemu. Konwersja wynika z faktu, że wektor normalny można zapisać jako liniową kombinację przykładów treningowych: ${\ displaystyle \ mathbf {w}}$

${\ Displaystyle \ mathbf {w} = \ suma _ {i = 1} ^ {m} \ alpha _ {i} y_ {i} \ mathbf {x} _ {i}}$

Formę podwójną uzyskuje się za pomocą mnożników Lagrange'a i warunków Karush-Kuhn-Tucker . To jest:

maksymalizować dla : ,${\ displaystyle \ mathbf {\ alpha}}$${\ Displaystyle \ sum _ {i = 1} ^ {m} \ alpha _ {i} - {\ Frac {1} {2}} \ sum _ {i = 1} ^ {m} \ sum _ {j = 1} ^ {m} \ alpha _ {i} \ alpha _ {j} y_ {i} y_ {j} \ langle \ mathbf {x} _ {i}, \ mathbf {x} _ {j} \ rangle}$

tak, aby ograniczenia i obowiązywały.${\ Displaystyle 0 \ równoważnik \ alfa _ {i} \ równoważnik C}$${\ Displaystyle \ sum _ {i = 1} ^ {m} \ alpha _ {i} y_ {i} = 0}$

Z tego wynika zasada klasyfikacji:

${\ displaystyle f (\ mathbf {x}) = \ operatorname {sgn} (\ langle \ mathbf {w, x} \ rangle + b) = \ operatorname {sgn} \ left (\ sum _ {i = 1} ^ {m} \ alpha _ {i} y_ {i} \ langle \ mathbf {x_ {i}, x} \ rangle + b \ right)}$

Nazwa SVM pochodzi od specjalnego podzbioru punktów szkoleniowych, które są zmiennymi Lagrange'a . Są one nazywane wektorami pomocniczymi i znajdują się na marginesie (jeśli ) lub wewnątrz marginesu ( ). ${\ displaystyle \ alpha _ {i} \ neq 0}$${\ Displaystyle y_ {i} (\ langle \ mathbf {w, x} \ rangle + b) = 1}$${\ displaystyle \ xi _ {i}> 0}$

Nieliniowe rozszerzenie z funkcjami jądra

Opisany powyżej algorytm klasyfikuje dane za pomocą funkcji liniowej. Jest to jednak optymalne tylko wtedy, gdy podstawowy problem klasyfikacji jest również liniowy. W wielu zastosowaniach tak nie jest. Jednym z możliwych sposobów jest zmapowanie danych w przestrzeni o wyższych wymiarach.

${\ Displaystyle \ phi \ colon \ mathbb {R} ^ {d_ {1}} \ rightarrow \ mathbb {R} ^ {d_ {2}}, \ mathbf {x} \ mapsto \ phi (\ mathbf {x}) }$

Obowiązują następujące zasady . To odwzorowanie zwiększa liczbę możliwych separacji liniowych (twierdzenie Covera). SVM charakteryzują się tym, że to rozszerzenie można bardzo elegancko zintegrować. Punkty danych są uwzględniane w iloczynach skalarnych tylko w problemie optymalizacji, na którym algorytm jest oparty w ostatnim sformułowaniu . Dlatego możliwe jest zastąpienie iloczynu wewnętrznego w przestrzeni wejściowej iloczynem wewnętrznym w i zamiast tego obliczenie go bezpośrednio. Koszt tego obliczenia można znacznie obniżyć, jeśli zamiast tego zostanie użyta pozytywnie zdefiniowana funkcja jądra : ${\ displaystyle d_ {1} <d_ {2}}$${\ displaystyle \ mathbf {x} _ {i}}$${\ displaystyle \ langle \ mathbf {x} _ {i}, \ mathbf {x} _ {j} \ rangle}$${\ displaystyle \ mathbb {R} ^ {d_ {1}}}$${\ displaystyle \ mathbb {R} ^ {d_ {2}}}$${\ Displaystyle \ langle \ phi (\ mathbf {x} _ {i}), \ phi (\ mathbf {x} _ {j}) \ rangle}$

${\ Displaystyle k (\ mathbf {x} _ {i}, \ mathbf {x} _ {j}) = \ langle \ phi (\ mathbf {x} _ {i}), \ phi (\ mathbf {x} _ {j}) \ rangle}$

Za pomocą tej metody można niejawnie obliczyć hiperpłaszczyznę (tj. Funkcję liniową) w przestrzeni wielowymiarowej. Wynikowy klasyfikator ma postać

${\ Displaystyle f (\ mathbf {x}) = \ operatorname {sgn} (\ langle \ mathbf {w}, \ mathbf {\ phi (x)} \ rangle + b) = \ operatorname {sgn} \ left (\ sum _ {i = 1} ^ {m} \ alpha _ {i} y_ {i} k (\ mathbf {x} _ {i}, \ mathbf {x}) + b \ right)}$

z . Korzystając z funkcji jądra , maszyny SVM mogą również działać na ogólnych strukturach, takich jak wykresy lub łańcuchy, i dlatego są bardzo wszechstronne. Chociaż potencjalnie nieskończenie wymiarowa przestrzeń jest domyślnie wykorzystywana przez mapowanie , SVM nadal bardzo dobrze generalizuje. Można wykazać, że oczekiwany błąd testu dla klasyfikatorów maksymalnych marginesów jest ograniczony i nie zależy od wymiarowości przestrzeni. ${\ Displaystyle \ textstyle \ mathbf {w} = \ suma _ {i = 1} ^ {m} \ alpha _ {i} y_ {i} \ phi (\ mathbf {x} _ {i})}$${\ displaystyle \ phi}$

historia

Ronald A. Fisher wpadł na pomysł separacji przez hiperpłaszczyznę już w 1936 roku . Podjął ją ponownie w 1958 r. Frank Rosenblatt w swoim wkładzie do teorii sztucznych sieci neuronowych . Idea maszyn wektorów nośnych sięga twórczości Władimira Wapnika i Aleksieja Jakowlewitscha Chervonenkisa . Na poziomie teoretycznym algorytm kieruje się zasadą strukturalnej minimalizacji ryzyka, która stwierdza, że ​​nie tylko błąd uczenia, ale także złożoność zastosowanego modelu determinuje zdolność uogólniania klasyfikatora. Maszyny SVM miały swój przełom w połowie lat 90., aw ostatnich latach opublikowano wiele ulepszeń i modyfikacji.

oprogramowanie

Biblioteki dla maszyn SVM

• libsvm , zaimplementowany w C ++ i przeniesiony na Javę
• liblinear , zaimplementowany w C ++ i przeportowany na Javę
• SVMlight na podstawie C

Oprogramowanie do uczenia maszynowego i eksploracji danych zawierające maszyny SVM

• GNU Octave używa SVMlight
• KNIME
• Matlab używa bibliotek libsvm , SVMlight i Spider
• RapidMiner wykorzystuje libsvm i SVM zaimplementowane w Javie
• Scikit-learn używa libsvm i liblinear .
• Shogun używa libsvm i SVMlight
• WEKA korzysta z libsvm i Spider

Moduły SVM do języków programowania (wybór)

• Perl ma moduły dla libsvm i SVMlight
• R , ma pakiety oparte na libsvm (pakiet e1071 ), SVMlight (pakiet klaR ) i ma pakiet kernlab do nauki jądra z SVM
• Ruby ma moduły dla libsvm i SVMlight

literatura

• Bernhard Schölkopf , Alex Smola: Learning with Kernels: Support Vector Machines, Regularization, Optimization, and Beyond (Adaptive Computation and Machine Learning) , MIT Press, Cambridge, MA, 2002, ISBN 0-262-19475-9 .
• Ingo Steinwart , Andreas Christmann: Support Vector Machines , Springer, Nowy Jork, 2008. ISBN 978-0-387-77241-7 . 602 s.
• Nello Cristianini, John Shawe-Taylor: Kernel Methods for Pattern Analysis , Cambridge University Press, Cambridge, 2004, ISBN 0-521-81397-2
• Christopher JC Burges: Tutorial on Support Vector Machines for Recognition Pattern , Data Mining and Knowledge Discovery, 2 (2): 121-167, 1998.
• Vladimir Vapnik : Statystyczna teoria uczenia się , Wiley, Chichester, GB, 1998.
• Vladimir Vapnik: The Nature of Statistical Learning Theory , Springer Verlag, Nowy Jork, NY, USA, 1995.

Indywidualne dowody

1. ↑ Schölkopf, Smola: Learning with Kernels, MIT Press, 2001
2. ↑ Fisher, RA (1936), „Zastosowanie wielu pomiarów w problemach taksonomicznych”, w Annals of Eugenics 7 : 179-188, doi : 10.1111 / j.1469-1809.1936.tb02137.x
3. ↑ Rosenblatt, F. (1958), „The Perceptron, a Probabilistic Model for Information Storage and Organisation in the Brain”, w: Psychological Review, 62/386, str. 386-408, doi : 10.1037 / h0042519 .
4. ↑ Vapnik and Chervonenkis, Theory of Pattern Recognition, 1974 (niemiecki przekład: Wapnik and Tschervonenkis, Theory of Pattern Recognition, 1979)
5. ^ David Meyer i wsp .: R-Paket e1071. Różne funkcje Departamentu Statystyki, Grupa Teorii Prawdopodobieństwa (dawniej: E1071), TU Wien. W: CRAN. The R Foundation, dostęp 14 maja 2016 (angielski, aktualna wersja: 1.6-7). 
6. ^ Uwe Ligges i in.: R-Paket klaR. Klasyfikacja i wizualizacja. W: CRAN. The R Foundation, dostęp 14 maja 2016 r. (Angielski, aktualna wersja: 0.6-12). 
7. ↑ Alexandros Karatzoglou, Alex Smola, Kurt Hornik: R-Paket kernlab. Laboratorium uczenia maszynowego oparte na jądrze. W: CRAN. The R Foundation, dostęp 14 maja 2016 (angielski, aktualna wersja: 0.9-24).