Rachunek całkowy

W uzupełnieniu do różniczkowego rachunku, całkowy jest najważniejszą gałęzią matematyki dyscypliny analizy . Powstał z problemu obliczania powierzchni i objętości . Integralną to ogólne określenie dla nieokreślony i określony całki. Obliczanie całek nazywa się całkowaniem.

Określony całka z funkcji przypisuje numer do niego. Jeżeli całka oznaczona funkcji rzeczywistej jest utworzona w zmiennej , to wynik można interpretować w dwuwymiarowym układzie współrzędnych jako pole powierzchni leżącej między wykresem funkcji, osią - i równoleżnikami granicznymi do -oś. W tym przypadku obszary poniżej osi są liczone jako ujemne. Mówi się o zorientowanej powierzchni (również o równowadze powierzchni ). Ta konwencja jest wybrana tak, że całka oznaczona jest odwzorowaniem liniowym${\ styl wyświetlania x}$${\ styl wyświetlania y}$${\ styl wyświetlania x}$jest tym, co reprezentuje centralną właściwość terminu całka zarówno w rozważaniach teoretycznych, jak i w konkretnych obliczeniach. Zapewnia to również zastosowanie tzw. głównego twierdzenia rachunku różniczkowego i całkowego .

Całka nieoznaczona z funkcji przypisuje to do wielu funkcji, elementy funkcji pierwotnych są nazywane. Charakteryzują się one tym, że ich pierwsze pochodne pasują do funkcji, która została zintegrowana. Główne twierdzenie rachunku różniczkowego i całkowego dostarcza informacji o tym, jak pewne całki można obliczyć z funkcji pierwotnych.

W przeciwieństwie do różniczkowania, nie ma prostego algorytmu obejmującego wszystkie przypadki całkowania nawet funkcji elementarnych . Całkowanie wymaga wyuczonego zgadywania, użycia specjalnych przekształceń ( całkowanie przez podstawienie , całkowanie częściowe ), patrzenia w całkową tabelę lub użycia specjalnego oprogramowania komputerowego. Całkowanie często odbywa się tylko w przybliżeniu za pomocą tzw. kwadratury numerycznej .

W technologii do przybliżonego wyznaczania powierzchni wykorzystuje się tzw. planimetry , w których sumowanie elementów powierzchni odbywa się w sposób ciągły. Tak wyznaczoną wartość liczbową powierzchni można odczytać na liczniku wyposażonym w noniusz w celu zwiększenia dokładności odczytu . Chemicy używali wagi analitycznej lub mikrowagi, aby określić całkę dowolnego obszaru : obszar został starannie wycięty i zważony, podobnie jak kawałek tego samego papieru o wymiarach dokładnie 10 cm × 10 cm ; reguła trzech doprowadziły do wyniku.

fabuła

Obliczenia powierzchni były badane od czasów starożytnych . W 5 wieku BC Eudoksos z Knidos opracowano w sposób wyczerpanie oparty na pomyśle Antyfona , który składał się z oszacowania do proporcji pola powierzchni za pomocą znajdujących się lub zachodzące na siebie wielokątów . Dzięki tej metodzie był w stanie określić zarówno powierzchnię, jak i objętość niektórych prostych ciał. Archimedes (287–212 p.n.e.) udoskonalił to podejście, dzięki czemu udało mu się precyzyjnie określić obszar obszaru ograniczonego łukiem parabolicznym i sieczną bez uciekania się do pojęcia granicy , które nie było wówczas jeszcze dostępne; wynik ten można łatwo przekształcić w całkę z funkcji kwadratowej znanej dzisiaj. Oszacował również stosunek obwodu do średnicy, jako wartość między a . ${\ styl wyświetlania \ pi}$${\ displaystyle \ textstyle {3 {\ frac {10} {71}}}}$${\ displaystyle \ textstyle {3 {\ frac {10} {70}}}}$

Ta metoda była również stosowana w średniowieczu. W 17 wieku, Bonawentura Francesco Cavalieri ustanowiony na zasadę Cavalieri , zgodnie z którym dwa ciała mają tę samą objętość, jeżeli wszystkie odcinki równoległe płaszczyzny mają taką samą powierzchnię. W swojej pracy Astronomia Nova (1609) Johannes Kepler wykorzystał metody obliczania orbity Marsa, które dziś określa się mianem całkowania numerycznego. Od 1612 r. próbował obliczyć objętość beczek z winem. W 1615 opublikował Stereometria Doliorum Vinariorum (" Stereometria beczek z winem"), później znaną również jako reguła beczki Keplera .

Pod koniec XVII wieku Isaacowi Newtonowi i Gottfriedowi Wilhelmowi Leibnizowi udało się niezależnie od siebie opracować rachunki dla rachunku różniczkowego, a tym samym odkryć fundamentalne twierdzenie analizy (historia odkrycia i spór o pierwszeństwo zob. artykuł Rachunek nieskończoności ; dla znaku całkowego i jego historii patrz znak całkowy ). Jej praca pozwoliła na abstrakcję idei czysto geometrycznych i dlatego jest uważana za początek analizy. Najbardziej znani są z książki szlachcica Guillaume François Antoine, markiza de L'Hospital , który pobierał prywatne lekcje u Johanna I Bernoulliego i publikował swoje badania na temat analizy. Termin całka pochodzi od Johanna Bernoulliego.

W XIX wieku cała analiza została postawiona na solidniejszym fundamencie. W 1823 Augustin-Louis Cauchy po raz pierwszy opracował integralny termin, który spełnia dzisiejsze wymagania dotyczące rygorystyczności . Terminy całki Riemanna i całki Lebesgue'a pojawiły się później . Wreszcie rozwój teorii miary nastąpił na początku XX wieku.

Integralny dla kompaktowych interwałów

„Kompaktowy” oznacza tutaj ograniczony i zamknięty, więc brane są pod uwagę tylko funkcje w odstępach formy . Otwarte lub nieograniczone odstępy czasu są niedozwolone. ${\ styl wyświetlania [a, b]}$

motywacja

Redukcja powierzchni złożonych do całek

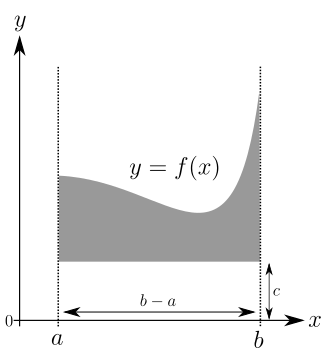
Jednym z celów rachunku całkowego jest obliczenie powierzchni krzywoliniowo ograniczonych obszarów płaszczyzny. W większości przypadków, które występują w praktyce, obszary takie są opisywane przez dwie ciągłe funkcje na zwartym przedziale , których wykresy ograniczają obszar (rysunek lewy). ${\ styl wyświetlania f, g}$${\ styl wyświetlania [a, b]}$

: :

Obszar szarego obszaru na lewym obrazie jest równy różnicy między szarymi obszarami na dwóch prawym obrazie. Wystarczy więc ograniczyć się do prostszego przypadku obszaru ograniczonego przez:

• wykres funkcji
• dwie pionowe linie proste i${\ styl wyświetlania x = a}$${\ styl wyświetlania x = b}$
• jak również oś.${\ styl wyświetlania x}$

Ze względu na swoje fundamentalne znaczenie obszarowi temu nadaje się specjalną nazwę:

${\ displaystyle \ int _ {a} ^ {b} f (x) \, \ mathrm {d} x}$,

odczytywane jako całka do około${\ styl wyświetlania a}$${\ styl wyświetlania b}$ (lub przez ) z , . Obecnie współczynnik jest powszechnie używany jako czysty składnik notacji i oznacza różnicę na osi -. Zamiast wybierać inną zmienną poza i np. co nie zmienia wartości całki. ${\ styl wyświetlania f}$${\ styl wyświetlania x}$${\ styl wyświetlania \ matematyka {d} x}$ ${\ styl wyświetlania \ matematyka {d} x}$${\ styl wyświetlania x}$${\ styl wyświetlania x}$${\ styl wyświetlania a}$${\ styl wyświetlania b}$${\ styl wyświetlania t}$

Integralne funkcje ujemne

Jeśli przesuniemy wykres funkcji w kierunku osi o bit , do rozważanego obszaru dodawany jest prostokąt: ${\ styl wyświetlania y}$${\ styl wyświetlania c}$

:

Całka zmienia się o obszar tego prostokąta szerokości i wysokości we wzorach ${\ displaystyle ba}$${\ styl wyświetlania c}$

${\ displaystyle \ int _ {a} ^ {b} (f (x) + c) \, \ mathrm {d} x = \ int _ {a} ^ {b} f (x) \, \ mathrm {d } x + (ba) \ cdot c.}$

Jeśli spojrzymy na funkcję ciągłą, której wartości są ujemne, zawsze można znaleźć a, więc wszystkie wartości w przedziale są dodatnie ( musi być większe niż wartość bezwzględna minimum in ). Z powyższych rozważań uzyskuje się ${\ displaystyle c \ in \ mathbb {R}}$${\ styl wyświetlania f (x) + c}$${\ styl wyświetlania c}$${\ styl wyświetlania f}$${\ styl wyświetlania [a, b]}$

${\ displaystyle \ int _ {a} ^ {b} f (x) \, \ matematyka {d} x = \ int _ {a} ^ {b} (f (x) + c) \, \ matematyka {d } x- (ba) \ cdot c,}$

oznacza to, że całka z jest różnicą między obszarami białego obszaru w środku i otaczającym go prostokątem. Różnica ta jest jednak ujemna, tzn. jeśli powyższy wzór ma być poprawny dla dowolnej funkcji, obszary poniżej osi muszą być liczone ujemnie. Mówi się zatem o obszarze zorientowanym lub ukierunkowanym . ${\ styl wyświetlania f}$${\ styl wyświetlania x}$

Jeśli w badanym przedziale występuje jedno lub więcej zer, całka nie wskazuje już pola, lecz sumę (dodatnich) pól cząstkowych powyżej osi - i (ujemnych) pól cząstkowych poniżej -działający. Jeśli potrzebujesz obszaru między osią - a wykresem funkcji w takim przedziale , całka musi zostać podzielona przez zera. ${\ styl wyświetlania x}$${\ styl wyświetlania x}$${\ styl wyświetlania x}$

Zasada Cavalieriego i addytywność całki

Podejście aksjomatyczne

Nie jest łatwo uchwycić pojęcie pola w matematycznie precyzyjny sposób. Z biegiem czasu opracowano w tym celu różne koncepcje. W przypadku większości zastosowań ich szczegóły są jednak nieistotne, ponieważ między innymi zgadzają się na klasę funkcji ciągłych. Poniżej wymieniono niektóre właściwości całki, które motywowano powyżej i które dotyczą każdej całki niezależnie od jej dokładnej konstrukcji. Ponadto jasno definiują całkę funkcji ciągłych.

Niech to będzie prawdziwe numery i niech to będzie przestrzenią liniową funkcji , które zawiera te ciągłe funkcje . Funkcje w programie są nazywane „integrowalnymi”. Wtedy całka jest odwzorowaniem ${\ styl wyświetlania a <b}$ ${\ displaystyle {\ matematyczne {F}}}$${\ displaystyle [a, b] \ do \ mathbb {R}}$${\ displaystyle {\ matematyczne {F}}}$

${\ displaystyle {\ mathcal {F}} \ do \ mathbb {R},}$

pisemny

${\ displaystyle f \ mapsto \ int _ {a} ^ {b} f (x) \, \ mathrm {d} x,}$

o następujących cechach:

• Liniowość: dla funkcji i zastosowań ${\ displaystyle f, g \ in {\ mathcal {F}}}$${\ displaystyle \ lambda \ in \ mathbb {R}}$
  • ${\ displaystyle \ int _ {a} ^ {b} (f (x) + g (x)) \, \ mathrm {d} x = \ int _ {a} ^ {b} f (x) \, \ mathm {d} x + \ int _ {a} ^ {b} g (x) \, \ mathrm {d} x}$,
  • ${\ displaystyle \ int _ {a} ^ {b} \ lambda f (x) \, \ mathrm {d} x = \ lambda \ cdot \ int _ {a} ^ {b} f (x) \, \ mathrm {d} x}$.
• Monotonia: jest dla wszystkich , tak samo ${\ styl wyświetlania f (x) \ geq 0}$${\ styl wyświetlania x \ w [a, b]}$

  ${\ displaystyle \ int _ {a} ^ {b} f (x) \, \ mathrm {d} x \ geq 0.}$

• Całka funkcji charakterystycznej przedziału: jest przedziałem i jest${\ displaystyle I \ subseteq [a, b]}$

${\ displaystyle \ chi _ {I} (x) = {\ początek {przypadki} 1 \, & \ mathrm {jeżeli} \ x \ in I \, \\ 0 \, & \ mathrm {jeżeli} \ x \ notin I \, \ koniec {przypadki}}}$

więc jest

${\ displaystyle \ int _ {a} ^ {b} \ chi _ {I} (x) \, \ matematyka {d} x}$

równy długości przedziału .${\ styl wyświetlania I}$

Oznaczenia

• Liczby rzeczywiste i nazywane są granicami integracji. Mogą być napisane powyżej i poniżej znaku całkowitego lub z boku znaku całkowitego:${\ styl wyświetlania a}$${\ styl wyświetlania b}$

${\ displaystyle {\ textstyle \ int \ limity _ {a} ^ {b}} f (x) \, {\ rm {d}} x}$     lub     ${\ displaystyle \ int \ nolimits _ {a} ^ {b} f (x) \, {\ rm {d}} x}$

• Funkcja, która ma zostać scałkowana, nazywana jest integrandem .${\ styl wyświetlania f}$
• Zmienna nazywana jest zmienną integrującą . Jeśli zmienną całkową jest, to mówi się również o integracji o . Zmienna integracyjna jest wymienna, zamiast${\ styl wyświetlania x}$${\ styl wyświetlania x}$${\ styl wyświetlania x}$

${\ displaystyle \ int _ {a} ^ {b} f (x) \, \ mathrm {d} x}$

równie dobrze możesz zrobić

${\ displaystyle \ int _ {a} ^ {b} f (t) \, \ mathrm {d} t}$ lub ${\ displaystyle \ int _ {a} ^ {b} f (\ xi) \, \ mathrm {d} \ xi}$

pisać. W powyższym przykładzie użycie liter lub prowadzi do niepożądanych niejasności, ponieważ pełnią one już rolę identyfikatorów granic integracji. Dlatego należy upewnić się, że znak używany w zmiennej integrującej nie ma już przypisanego innego znaczenia.${\ styl wyświetlania a}$${\ styl wyświetlania b}$

• Składnik „ ” nazywa się różnicą , ale w tym kontekście ma głównie znaczenie symboliczne. Dlatego nie podejmuje się tutaj żadnej próby jej zdefiniowania. Zmienną całkową można odczytać z różniczki.${\ styl wyświetlania \ matematyka {d} x}$

Pochodzenie notacji

Symboliczna pisownia całek sięga współpierwszego deskryptora rachunku różniczkowego i całkowego, Gottfrieda Wilhelma Leibniza . Integralny znak ∫ pochodzi z listu długo s (y) Łacińskiej Summa . Notacja multiplikatywna wskazuje, w jaki sposób całka - po całce Riemanna - składa się z pasków o wysokości i nieskończenie małej szerokości . ${\ displaystyle f (x) \; \ mathrm {d} x}$${\ styl wyświetlania f (x)}$${\ styl wyświetlania \ matematyka {d} x}$

Alternatywna pisownia w fizyce

W fizyce teoretycznej, ze względów pragmatycznych, często stosuje się nieco inny zapis dla całek (zwłaszcza dla całek wielokrotnych). Odbywa się

${\ displaystyle \ int _ {a} ^ {b} f (x) \, \ mathrm {d} x}$

często

${\ displaystyle \ int _ {a} ^ {b} \ matematyka {d} xf (x)}$

czasami obie pisownie są używane w różnych miejscach.

W drugim przykładzie ma tę wadę, że jest zintegrowana funkcja nie przez i ujęty. Ponadto mogą wystąpić nieporozumienia , na przykład z całką Lebesgue'a . Jednak alternatywna notacja ma również pewne zalety: ${\ styl wyświetlania f (x)}$${\ styl wyświetlania \ styl tekstu \ int _ {a} ^ {b}}$${\ styl wyświetlania \ matematyka {d} x}$

• Wyrażenie podkreśla, że ​​całka jest operatorem liniowym, który działa na wszystko na prawo od niej.${\ displaystyle \ textstyle \ int _ {a} ^ {b} \ mathrm {d} x}$
• W fizyce często pojawiają się całki, w których funkcja, która ma być całkowana, ma długość kilku linii lub jest całkowana przez kilka niewiadomych . Wtedy już wiesz, na początku całki, które zmienne są całkowane i nad którymi granicami z notacją . Ponadto przypisanie zmiennych do limitów jest wtedy łatwiejsze.${\ styl wyświetlania x_ {1}, x_ {2}, \ kropka, x_ {n}}$${\ displaystyle \ textstyle \ int _ {a} ^ {b} \ mathrm {d} xf (x)}$
• Podkreślono przemienność produktów w sumach występujących w przybliżeniu Riemanna .${\ styl wyświetlania \ Delta x_ {n} \ cdot f (x_ {n})}$

Przykład:

${\ displaystyle \ int _ {a_ {1}} ^ {a_ {2}} \ mathm {d} t \ int _ {b_ {1}} ^ {b_ {2}} \ mathrm {d} x_ {1} \ int _ {c_ {1}} ^ {c_ {2}} \ mathm {d} x_ {2} \ int _ {d_ {1}} ^ {d_ {2}} \ mathrm {d} x_ {3} \, f (x_ {1}, x_ {2}, x_ {3}, t)}$

zamiast

${\ displaystyle \ int _ {a_ {1}} ^ {a_ {2}} \ int _ {b_ {1}} ^ {b_ {2}} \ int _ {c_ {1}} ^ {c_ {2} } \ int _ {d_ {1}} ^ {d_ {2}} f (x_ {1}, x_ {2}, x_ {3}, t) \, \ mathm {d} x_ {3} \ mathm { d} x_ {2} \ matematyka {d} x_ {1} \ matematyka {d} t}$

Proste wnioski z aksjomatów

• Jest dla wszystkich , więc jest${\ styl wyświetlania f (x) \ leq g (x)}$${\ displaystyle a \ leq x \ leq b}$

${\ displaystyle \ int _ {a} ^ {b} f (x) \, \ mathrm {d} x \ leq \ int _ {a} ^ {b} g (x) \, \ mathrm {d} x. }$

• Jeśli ktoś wskazuje na normę Supremum z na , a następnie stosuje się następującą${\ displaystyle \ | f \ | _ {\ infty}}$${\ styl wyświetlania f}$${\ styl wyświetlania [a, b]}$

${\ displaystyle \ left | \ int _ {a} ^ {b} f (x) \, \ mathrm {d} x \ right | \ leq (ba) \ cdot \ | f \ | _ {\ infty}.}$

• Czy dla wszystkich ze stałą liczbą , to obowiązuje${\ styl wyświetlania | f (x) -g (x) | <\ varepsilon}$${\ displaystyle a \ leq x \ leq b}$${\ styl wyświetlania \ varepsilon> 0}$

${\ displaystyle \ lewo | \ int _ {a} ^ {b} f (x) \, \ mathrm {d} x- \ int _ {a} ^ {b} g (x) \, \ mathrm {d} x \ right | \ leq (ba) \ cdot \ varepsilon.}$

Wynika z tego: Jeśli sekwencja funkcji całkowalnych, która zbiega się jednostajnie do funkcji (całkowalnej) , to jest ${\ displaystyle (f_ {n}) _ {n \ in \ mathbb {N}}}$${\ styl wyświetlania f}$

${\ displaystyle \ lim _ {n \ do \ infty} \ int _ {a} ^ {b} f_ {n} (x) \, \ mathrm {d} x = \ int _ {a} ^ {b} f (x) \, \ matematyka {d} x.}$

Innymi słowy: całka jest funkcjonałem ciągłym dla normy najwyższej.

• Całki funkcji krok: Jeśli funkcja krok , to znaczy jest unia rozłączne z przerwami długości , tak, że on jest stała o wartości , wówczas stosuje się${\ styl wyświetlania f}$${\ styl wyświetlania [a, b]}$${\ styl wyświetlania I_ {k}}$${\ styl wyświetlania L_ {k}}$${\ styl wyświetlania f}$${\ styl wyświetlania I_ {k}}$${\ styl wyświetlania c_ {k}}$

${\ displaystyle \ int _ {a} ^ {b} f (x) \, \ mathrm {d} x = \ suma _ {k = 1} ^ {n} L_ {k} \ cdot c_ {k},}$

zatem wyraźnie równa sumie zorientowanych obszarów prostokątów między wykresem funkcji a osią.${\ styl wyświetlania f}$${\ styl wyświetlania x}$

Funkcje pierwotne i główne twierdzenie rachunku różniczkowego i całkowego

Integracja jest niejednoznacznym odwróceniem zróżnicowania. Aby to bardziej precyzyjne pojęcie pierwotna jest wymagane: Jeśli funkcja jest następnie wywoływana jest funkcja pierwotna of jeżeli pochodna od jest równa : ${\ styl wyświetlania f}$${\ styl wyświetlania F}$${\ styl wyświetlania f}$${\ styl wyświetlania F}$${\ styl wyświetlania f}$

${\ styl wyświetlania F '= f}$

Ta inwersja jest niejednoznaczna, ponieważ różne funkcje (np. funkcje wielomianowe, które różnią się tylko punktem przecięcia osi Y) mogą mieć jedną i tę samą pochodną, ​​co oznacza, że ​​funkcja ma nie tylko jedną, ale nieskończoną liczbę funkcji pierwotnych.

Główny twierdzenie różnicowej i całkowego ustanawia zależność między funkcja pierwotna i całki. Mówi: Jeśli jest funkcją ciągłą na przedziale i jest pierwotna stanowi , to mamy ${\ styl wyświetlania f}$${\ styl wyświetlania [a, b]}$${\ styl wyświetlania F}$${\ styl wyświetlania f}$

${\ displaystyle \ int _ {a} ^ {b} f (x) \, \ mathrm {d} x = F (b) -F (a).}$

Prawa strona jest często skracana jako

${\ displaystyle [F (x)] _ {a} ^ {b} = [F (x)] _ {x = a} ^ {x = b} = F (x) {\ Duży |} _ {a} ^ {b} = F (x) {\ Duży |} _ {x = a} ^ {x = b}}$ lub podobne

pisemny.

Ta zależność jest główną metodą jawnej oceny całek. Trudność zwykle polega na znalezieniu funkcji pierwotnej.

Samo istnienie jest teoretycznie zabezpieczone: funkcja całkowa

${\ displaystyle x \ mapsto \ int _ {a} ^ {x} f (t) \, \ mathrm {d} t}$

jest dla każdego pochodną . ${\ styl wyświetlania a}$${\ styl wyświetlania f}$

Właściwości instrumentów pierwotnych

Możesz dodać stałą do funkcji pierwotnej i ponownie uzyskać funkcję pierwotną: Jeśli funkcja pierwotna odnosi się do funkcji i jest stałą, to jest ${\ styl wyświetlania F}$${\ styl wyświetlania f}$${\ displaystyle c \ in \ mathbb {R}}$

${\ displaystyle (F + c) '= F \! \,' + 0 = F '= f.}$

Dwie funkcje pierwotne tej samej funkcji zdefiniowane na przedziale różnią się stałą: Jeśli i funkcje pierwotne tej samej funkcji , to jest ${\ styl wyświetlania F}$${\ styl wyświetlania G}$${\ styl wyświetlania f}$

${\ styl wyświetlania (FG) \! \, '= F'-G' = ff = 0,}$

więc różnica jest stała. Jeżeli domena z definicji jest nie odstęp, to różnica między dwoma funkcja pierwotna jest tylko lokalnie stała . ${\ styl wyświetlania FG}$${\ styl wyświetlania f}$

Całka nieoznaczona

Funkcja pierwotna jest również określana jako całka nieoznaczona z - ale czasami oznacza również zbiór wszystkich funkcji pierwotnych. Jeśli jest pierwotna, często jest napisana nieprecyzyjnie ${\ styl wyświetlania f (x)}$${\ styl wyświetlania F (x)}$

${\ displaystyle \ int f (x) \, \ mathrm {d} x = F (x) + C,}$

aby wskazać, że każda funkcja pierwotna od ma postać ze stałą . Stałą nazywamy stałą integracji.${\ styl wyświetlania f}$${\ styl wyświetlania F (x) + C}$${\ styl wyświetlania C}$${\ styl wyświetlania C}$

Zauważ, że notacja

${\ styl wyświetlania \ int f (x) \, \ mathrm {d} x}$

jednak jest również często używany we wzorach, aby wskazać, że równania obowiązują dla dowolnych, konsekwentnie wybranych granic; na przykład jest z

${\ displaystyle \ int cf (x) \, \ mathrm {d} x = c \ int f (x) \, \ mathrm {d} x}$

miał na myśli

${\ displaystyle \ int _ {a} ^ {b} cf (x) \, \ mathrm {d} x = c \ int _ {a} ^ {b} f (x) \, \ mathrm {d} x}$

obowiązuje dla każdego . ${\ styl wyświetlania a, b}$

Oznaczanie pochodnych

Zobacz artykuł: Tablica pochodnych i funkcji pierwotnych lub całek nieoznaczonych w zbiorze formuł matematycznych .

W przeciwieństwie do funkcji pochodnej, jawne obliczenie funkcji pierwotnej jest bardzo trudne lub niemożliwe dla wielu funkcji. Dlatego całki są często wyszukiwane w tablicach (np. tablica całkowa ). Przy ręcznym obliczaniu funkcji pierwotnej często pomocne jest umiejętne użycie następujących standardowych technik.

Częściowa integracja

Całkowanie częściowe jest odwrotnością zasady iloczynu rachunku różniczkowego. To jest:

${\ displaystyle \ int _ {a} ^ {b} f '(x) \ cdot g (x) \, \ mathrm {d} x = [f (x) \ cdot g (x)] _ {a} ^ {b} - \ int _ {a} ^ {b} f (x) \ cdot g '(x) \, \ mathrm {d} x}$

Ta reguła jest przydatna, gdy funkcja jest łatwiejsza do zintegrowania niż funkcja . Tutaj jednak ocenia się produkty, a nie same czynniki. ${\ displaystyle f (x) \ cdot g '(x)}$${\ displaystyle f '(x) \ cdot g (x)}$

Przykład:

${\ displaystyle \ int _ {a} ^ {b} x \ ln (x) \, \ mathrm {d} x}$

Jeśli ustawisz

${\ displaystyle f '(x) = x \,}$ oraz ${\ styl wyświetlania g (x) = \ ln (x) \,}$

więc jest

${\ displaystyle f (x) = {\ frac {x ^ {2}} {2}}}$ oraz ${\ displaystyle g '(x) = {\ frac {1} {x}}}$

i dostajesz

${\ displaystyle {\ zacząć {wyrównany} \ int _ {a} ^ {b} x \ ln (x) \, \ mathrm {d} x & = {\ frac {b ^ {2}} {2}} \ ln (b) - {\ frac {a ^ {2}} {2}} \ ln (a) - \ int _ {a} ^ {b} {\ frac {x ^ {2}} {2}} \ cdot {\ frac {1} {x}} \, \ mathrm {d} x \\ & = {\ frac {b ^ {2}} {2}} \ lewo (\ ln (b) - {\ frac { 1 } {2}} \ po prawej) - {\ frac {a ^ {2}} {2}} \ po lewej (\ ln (a) - {\ frac {1} {2}} \ po prawej). \ Koniec { wyrównane }}}$

Integracja przez substytucję

Reguła podstawienia jest ważnym narzędziem do obliczania niektórych trudnych całek, ponieważ pozwala na całkowanie pewnych zmian funkcji przy zmianie granic całkowania. Jest to odpowiednik reguły łańcucha w rachunku różniczkowym.

Niech z i bądź pierwotną , to jest pierwotną , ponieważ posiada ${\ displaystyle \ varphi (x) = f (g (x)) \ cdot g '(x)}$${\ styl wyświetlania g '\ neq 0}$${\ styl wyświetlania F}$${\ styl wyświetlania f}$${\ styl wyświetlania \ Phi (x) = F (g (x))}$${\ styl wyświetlania \ varphi}$

${\ displaystyle {\ frac {\ varphi (x)} {g '(x)}} = f (g (x))}$

i z podmianą

${\ displaystyle z = g (x), \ quad \ mathm {d} z = g '(x) \ mathrm {d} x}$

na końcu

${\ displaystyle {\ zacząć {wyrównany} \ int _ {a} ^ {b} f (g (x)) g '(x) \ matematyka {d} x & = \ int _ {g (a)} ^ { g (b)} f (z) \ mathrm {d} z \\ & = F (g (b)) - F (g (a)) \\ & = \ Phi (b) - \ Phi (a). \ koniec {wyrównany}}}$

Przekształcanie poprzez częściowy rozkład frakcji

W przypadku funkcji ułamkowo-wymiernych dzielenie wielomianowe lub dekompozycja na ułamek częściowy często prowadzi do przekształcenia funkcji, co pozwala na zastosowanie jednej z reguł całkowania.

Procedury specjalne

Często możliwe jest określenie funkcji pierwotnej za pomocą specjalnej formy całki.

Inną możliwością jest rozpoczęcie od znanej całki i przekształcanie jej za pomocą technik całkowania, aż do uzyskania pożądanej całki. Przykład:

Aby to ustalić, całkujemy częściowo następującą podobną całkę: ${\ displaystyle \ textstyle \ int {\ frac {\ matematyka {d} x} {(1 + x ^ {2}) ^ {2}}}}$

${\ displaystyle {\ początek {wyrównany} \ arctan x & = \ int 1 \ cdot {\ frac {1} {1 + x ^ {2}}} \, \ mathrm {d} x \\ & = x \ cdot { \ frac {1} {1 + x ^ {2}}} + \ int x \ cdot {\ frac {2x} {(1 + x ^ {2}) ^ {2}}} \, \ mathrm {d } x \\ & = {\ frac {x} {1 + x ^ {2}}} + \ int \ lewo ({\ frac {2x ^ {2}} {(1 + x ^ {2}) ^ { 2 }}} + {\ frac {2} {(1 + x ^ {2}) ^ {2}}} \ prawy) \, \ mathrm {d} x- \ int {\ frac {2} {(1 + x ^ {2}) ^ {2}}} \, \ mathrm {d} x \\ & = {\ frac {x} {1 + x ^ {2}}} + 2 \ int {\ frac {1 + x ^ {2}} {(1 + x ^ {2}) ^ {2}}} \, \ mathrm {d} x-2 \ int {\ frac {1} {(1 + x ^ {2} ) ^ {2}}} \, \ mathrm {d} x \\ & = {\ frac {x} {1 + x ^ {2}}} + 2 \ arctan x-2 \ int {\ frac {\ mathrm { d} x} {(1 + x ^ {2}) ^ {2}}} \ koniec {wyrównany}}}$

Zmieniając to następuje

${\ displaystyle \ int {\ frac {\ mathrm {d} x} {(1 + x ^ {2}) ^ {2}}} = {\ frac {1} {2}} \ lewo ({\ frac { x} {1 + x ^ {2}}} + \ arctan x \ prawy).}$

Wielokrotna integracja

Jeśli funkcja ma być całkowana wielokrotnie, wzór Cauchy'ego dla całkowania wielokrotnego zapewnia -tę iterowaną całkę w punkcie${\ styl wyświetlania f}$${\ styl wyświetlania n}$${\ styl wyświetlania f}$${\ styl wyświetlania x}$

${\ displaystyle I ^ {n} (x) = \ int _ {a} ^ {x} \ int _ {a} ^ {\ sigma _ {1}} \ cdots \ int _ {a} ^ {\ sigma _ {n-1}} f (\ sigma _ {n}) \, \ mathrm {d} \ sigma _ {n} \ cdots \, \ mathrm {d} \ sigma _ {2} \, \ mathrm {d} \ sigma _ {1}}$

następująca całka:

${\ displaystyle I ^ {n} (x) = {\ frac {1} {(n-1)!}} \ int _ {a} ^ {x} \ po lewej (xt \ po prawej) ^ {n-1} f (t) \, \ mathm {d} t}$.

Aplikacje

Wartości średnie funkcji ciągłych

Aby obliczyć średnią wartość danej funkcji ciągłej na przedziale, używa się wzoru ${\ styl wyświetlania m}$ ${\ styl wyświetlania f}$ ${\ styl wyświetlania [a, b]}$

${\ displaystyle m = {\ frac {1} {ba}} \ int _ {a} ^ {b} f (x) \ mathrm {d} x.}$

Od tej definicji na schody funkcji odpowiada zwykłym pojęciem wartości średniej, to uogólnienie jest przydatna.

Średnia wartość twierdzenie rachunku całkowego mówi, że średnia wartość jest rzeczywiście zakłada ciągłą funkcji w przedziale . ${\ styl wyświetlania [a, b]}$

Przykład terminu całka w fizyce

Fizyczny zjawisko , które można wykorzystać, aby wyjaśnić pojęcie całki jest swobodny spadek w organizmie w tego ziemskiego pola grawitacyjnego . Przyspieszenie od swobodnego spadania w Europie Środkowej wynosi ok. 9,81 m / s². Prędkość ciała w czasie może być zatem wyrażony wzorem ${\ styl wyświetlania g}$ ${\ styl wyświetlania v}$${\ styl wyświetlania t}$

${\ styl wyświetlania v = g \ cdot t}$

wyrazić.

Ale teraz należy obliczyć odległość , jaką spadające ciało pokonuje w określonym czasie . Problem polega na tym, że z czasem prędkość ciała wzrasta. W celu rozwiązania problemu zakłada się, że przez krótki czas prędkość wynikająca z czasu pozostaje stała. ${\ styl wyświetlania l}$${\ styl wyświetlania T}$${\ styl wyświetlania v}$${\ styl wyświetlania \ Delta t}$${\ styl wyświetlania v}$${\ styl wyświetlania g \ cdot t}$

Wzrost odległości podróży w krótkim okresie jest zatem ${\ styl wyświetlania \ Delta t}$

${\ Displaystyle \ Delta l = g \ cdot t \, \ cdot \ Delta t}$.

Całą odległość można zatem opisać jako

${\ displaystyle l = \ suma \ lewo (g \ cdot t \, \ cdot \ Delta t \ po prawej)}$

wyrazić. Jeśli teraz pozwolisz, aby różnica czasu zbliżała się do zera, uzyskasz ${\ styl wyświetlania \ Delta t}$

${\ displaystyle l = \ lim _ {\ Delta t \ do 0} \ po lewej (\ suma \ po lewej (g \ cdot t \, \ cdot \ Delta t \ po prawej) \ po prawej) = \ int _ {0} ^ { T} \ left (g \ cdot t \; \ mathrm {d} t \, \ right).}$

Całkę można podać analitycznie za pomocą

${\ displaystyle l = \, {\ frac {g} {2}} \ cdot T ^ {2}.}$

Ogólne rozwiązanie prowadzi do równania ruchu ciała w stałym polu grawitacyjnym:

${\ displaystyle l = {\ frac {g} {2}} \ cdot t ^ {2}}$

Ponadto z tego równania ruchu, różniczkując po czasie, równanie prędkości może być:

${\ styl wyświetlania v = g \ cdot t}$

i wyprowadź przez ponowne różniczkowanie dla przyspieszenia:

${\ styl wyświetlania a = g}$

Inne proste przykłady to:

• Energia jest całka siły w czasie.
• Ładunek elektryczny z kondensatora jest całka prądu przepływającego przez niego w czasie.
• Całka iloczynu irradiancji widmowej ( E _e ( ν ) w W / m ² Hz ) z krzywą światłoczułości spektralnej oka daje natężenie oświetlenia ( E w luksach = lumen / m ² ).
• Całka prędkości przepływu (składowa podłużna) przez przekrój rury zapewnia cały przepływ objętościowy przez rurę (dalsze całki wielowymiarowe patrz poniżej ).

Konstrukcje

Całka Cauchy'ego

Funkcja sterująca to funkcja, którą można aproksymować równomiernie za pomocą funkcji krokowych . Ze względu na wspomnianą wcześniej zgodność całki z granicami jednorodnymi, dla funkcji sterującej, która jest granicą jednolitą ciągu funkcji skokowych, całkę można zdefiniować jako ${\ styl wyświetlania f}$${\ styl wyświetlania t_ {n}}$

${\ displaystyle \ int _ {a} ^ {b} f (x) \, \ mathrm {d} x = \ lim _ {n \ do \ infty} \ int _ {a} ^ {b} t_ {n} (x) \, \ matematyka {d} x,}$

gdzie całka dla funkcji skokowych jest określona wzorem podanym powyżej.

Klasa funkcji sterowania obejmuje wszystkie ciągłe funkcje i wszystkich funkcji, monotoniczne , a także wszystkie funkcje , dla których mogą być podzielone na skończoną liczbę przedziałów tak, że ograniczenie w celu ciągłego i jest funkcją monotonicznie w zamkniętym przedziale , tj H. wszystkie odcinkowo ciągłe funkcje. Obejmuje również funkcje o ograniczonej zmienności , ponieważ taką funkcję można przedstawić jako różnicę między dwiema monotonicznie rosnącymi funkcjami. Z wielu praktycznych celów ta integralna konstrukcja jest w zupełności wystarczająca. ${\ styl wyświetlania f}$${\ styl wyświetlania [a, b]}$${\ styl wyświetlania I_ {k}}$${\ styl wyświetlania f}$${\ styl wyświetlania I_ {k}}$${\ displaystyle {\ bar {I}} _ {k}}$

Istnieją również funkcje ciągłe o nieskończonej zmienności, takie jak B. funkcja zdefiniowana przez i dla na przedziale (patrz wariacja ). ${\ styl wyświetlania 0 \ mapsto 0}$${\ displaystyle t \ mapsto t \ cos {\ tfrac {\ pi/2} {t}}}$${\ styl wyświetlania 0 <t \ leq 1}$${\ styl wyświetlania [0,1]}$

Całka Riemanna

Jednym ze sposobów obliczania całki według Riemanna jest aproksymacja całkowanej funkcji przez funkcję skokową ; jednak nie przez równomierne przybliżenie samej funkcji, ale przez przybliżenie pola za pomocą sum prostokątnych.

Powierzchnia jest aproksymowana przez sumę powierzchni poszczególnych prostokątów pod poszczególnymi „krokami”. Dla każdego podziału przedziału całkowania można wybrać dowolną wartość funkcji w każdym podprzedziale jako poziom poziomu.

Są to na cześć niemieckiego matematyka Bernharda Riemanna, który nazwał sumami Riemanna. Jeśli jeden wybiera Supremum z funkcji jako wysokość prostokąta, w każdym sub-przedziału rozkładu , to górna Podsumowując, wyniki z infimum niższej sumy.

Całkę Riemanna można zdefiniować za pomocą sum górnych i dolnych, patrz całka Riemanna. Jeżeli suma górna i dolna zbiegają się do tej samej wartości granicznej , ta wartość graniczna jest całką w sensie Riemanna. Całkowite w tym sensie są z. B. wszystkie funkcje, dla których istnieje całka Cauchy'ego.

Riemanna integralną istnieje np B. nie dla funkcji wskaźnikowej liczb wymiernych w przedziale , tj. H. dla funkcji Dirichleta . Dlatego rozszerzone terminy całkowe wprowadzili Henri Léon Lebesgue ( całka Lebesgue'a ), Thomas Jean Stieltjes ( całka Stieltjesa ) i Alfréd Haar , którzy odtwarzają całkę Riemanna dla całki ciągłej. ${\ styl wyświetlania [0,1]}$

Całka Stieltjesa

Całka Stieltjesa opiera się na funkcjach monotonicznych lub tych o skończonej zmienności , czyli różnicach między dwiema funkcjami monotonicznymi, a sumy Riemanna-Stieltjesa są zdefiniowane dla funkcji ciągłych jako ${\ styl wyświetlania g (x)}$${\ styl wyświetlania f}$

${\ displaystyle \ suma _ {i = 0} ^ {n-1} \, f (x_ {i}) \, \ {g (x_ {i + 1}) - g (x_ {i}) \}. }$

Tak zwana całka Riemanna-Stieltjesa jest następnie otrzymywana przez utworzenie granicy w zwykły sposób . ${\ displaystyle \ textstyle \ int _ {I} \, f \, \ mathrm {d} g}$

Takie całki są również zdefiniowane, jeśli funkcja nie jest różniczkowalna (w przeciwnym razie obowiązuje ). Dobrze znanym kontrprzykładem jest tak zwana funkcja Heaviside'a , której wartość wynosi zero dla liczb ujemnych, jeden dla dodatnich iz. B. o pkt . Pisze się dla iw ten sposób otrzymuje „funkcję uogólnioną” , tak zwaną miarę Diraca , jako miarę zdefiniowaną tylko dla punktu . ${\ styl wyświetlania g}$${\ displaystyle \ mathrm {d} g \ równoważnik g '(x) \, \ mathrm {d} x}$ ${\ styl wyświetlania \ Theta (x)}$${\ styl wyświetlania x}$${\ styl wyświetlania = 1/2}$${\ styl wyświetlania x = 0}$${\ styl wyświetlania g (x) = \ Theta (x),}$ ${\ styl wyświetlania \ matematyka {d} g = \ delta (x) \ matematyka {d} x}$ ${\ styl wyświetlania \ delta (x)}$${\ styl wyświetlania x = 0}$

Całka Lebesgue'a

Całka Lebesgue'a dostarcza bardziej nowoczesnego i - pod wieloma względami - lepszego członu całkowego niż całka Riemanna. Na przykład umożliwia integrację przy użyciu ogólnych przestrzeni wymiarowych . Oznacza to, że ilościom można przypisać miarę , która niekoniecznie musi odpowiadać ich geometrycznej długości lub objętości, na przykład miarom prawdopodobieństwa w teorii prawdopodobieństwa . Miarą, która odpowiada intuicyjnemu pojęciu długości lub objętości, jest miara Lebesgue'a . Z reguły całkę nad tym wymiarem nazywamy całką Lebesgue'a . Można udowodnić, że dla każdej funkcji, która jest całkowalna Riemanna na przedziale zwartym, istnieje również odpowiednia całka Lebesgue'a i wartości obu całek są zgodne. Odwrotnie jednak, nie wszystkie funkcje całkowalne Lebesgue'a są również całkowalne Riemanna. Najbardziej znanym tego przykładem jest funkcja Dirichleta , czyli funkcja, która ma wartość jeden dla liczb wymiernych, ale wartość zero dla liczb niewymiernych. Oprócz większej klasy funkcji całkowalnych, całka Lebesgue'a różni się od całki Riemanna przede wszystkim twierdzeniami o lepszej zbieżności ( twierdzenie o zbieżności monotonicznej , twierdzenie o zbieżności majoryzowanej ) oraz lepszymi własnościami przestrzeni funkcyjnych znormalizowanych przez całkę Lebesgue'a ( w przybliżeniu kompletność ).

We współczesnej matematyce, teoria całkowa lub integracyjna jest często rozumiana jako całkowy termin Lebesgue'a.

Niewłaściwa integralność

Całka Riemanna jest (w przestrzeni jednowymiarowej) zdefiniowana tylko dla przedziałów zwartych , tj. ograniczonych i domkniętych . Całka niewłaściwa oferuje uogólnienie na nieograniczone dziedziny definicji lub funkcji z osobliwościami . W teorii Lebesgue'a można również rozważać całki niewłaściwe, ale nie jest to tak produktywne, ponieważ całka Lebesgue'a może już integrować wiele funkcji z osobliwościami lub dziedziną nieograniczoną.

Metoda obliczania całek oznaczonych i niewłaściwych

Metody numeryczne

Wyraźne określenie funkcji pierwotnej jest często trudne lub niemożliwe. Jednak w wielu przypadkach wystarczy w przybliżeniu obliczyć całkę właściwą. Następnie mówi się o kwadraturze numerycznej lub całkowaniu numerycznym . Wiele metod obliczania kwadratury numerycznej opiera się na aproksymacji funkcji funkcjami łatwiejszymi do całkowania, na przykład wielomianami. Przykładami tego są reguła trapezów lub wzór Simpsona (których szczególny przypadek znany jest jako reguła beczki Keplera ), tutaj wielomian interpolacyjny jest umieszczany przez funkcję, a następnie całkowany.

Na długo przed rozpowszechnieniem się komputerów opracowano metody automatycznej kontroli wielkości kroku do integracji numerycznej . Obecnie algebra komputerowa daje możliwość numerycznego rozwiązywania złożonych całek w coraz krótszych czasach lub przy coraz bardziej precyzyjnych rozwiązaniach, przy czym nawet w potężnych systemach nadal występują trudności z niewłaściwymi całkami, do obliczania których często mają specjalne metody, takie jak Gauss-Kronrod. być używana. Przykładem takiej twardej całki jest:

${\ displaystyle \ int _ {0} ^ {\ infty} {\ frac {\ ln (1 + x)} {\ ln ^ {2} x + \ pi ^ {2}}} \ cdot {\ frac {\ mathm {d} x} {x ^ {2}}} = \ gamma}$

Metody klasyczne to m.in. B. Wzór empiryczny Eulera , w którym całka oznaczona jest aproksymowana szeregiem ogólnie asymptotycznym . Inne metody opierają się na teorii rachunku różnic , ważnym przykładem, o którym należy tu wspomnieć, jest formuła całkowa Gregory'ego.

Dokładne procedury

Istnieje wiele metod, za pomocą których całki oznaczone i niewłaściwe można obliczyć dokładnie w postaci symbolicznej.

Jeśli znana jest ciągła i funkcja pierwotna , całka oznaczona może być ${\ styl wyświetlania f}$${\ styl wyświetlania f}$${\ styl wyświetlania F}$

${\ displaystyle \ int _ {a} ^ {b} f (x) \, \ mathrm {d} x = F (b) -F (a)}$

obliczyć według klauzuli głównej. Problem w tym, że działanie nieskończonej integracji prowadzi do rozszerzenia danych klas funkcjonalnych. Na przykład integracja w obrębie klasy funkcji wymiernych nie jest kompletna i prowadzi do funkcji i . Nie jest też zamknięta klasa tzw. funkcji elementarnych . W ten sposób Joseph Liouville udowodnił, że funkcja nie ma elementarnej funkcji pierwotnej. Leonhard Euler był jednym z pierwszych, którzy opracowali metody dokładnego obliczania pewnych i niewłaściwych całek bez określania funkcji pierwotnej. Z biegiem czasu pojawiło się wiele bardziej ogólnych i szczegółowych metod specyficznej integracji: ${\ styl wyświetlania \ ln}$${\ styl wyświetlania \ arctan}$${\ styl wyświetlania e ^ {- x ^ {2}}}$

• Korzystanie z twierdzenia resztkowego
• Reprezentacja całki zależnej od parametru przez funkcje specjalne
• Różniczkowanie lub całkowanie całki według parametru i zamiana procesów brzegowych
• Wykorzystanie szeregowego rozszerzenia integrandu z integracją przez term
• zredukować całkę do siebie lub do innej poprzez częściową integrację i substytucję

Pod koniec XX wieku powstały liczne (niekiedy wielotomowe) tablice całkowe z pewnymi całkami. Kilka przykładów ilustrujących problem:

${\ displaystyle \ int _ {0} ^ {1} {\ frac {\ ln (1 + x)} {x ^ {2} +1}} \, \ mathrm {d} x = {\ frac {\ pi } {8}} \ w 2}$

${\ displaystyle \ int _ {0} ^ {\ pi} \ ln \ sin x \, \ mathrm {d} x = - \ pi \ ln 2}$

Całki specjalne

Istnieje wiele całek oznaczonych i niewłaściwych, które mają określone znaczenie dla matematyki i dlatego mają swoją własną nazwę:

• Całki Eulera pierwszego i drugiego rodzaju
• Całka błędu Gaussa

${\ displaystyle \ int _ {- \ infty} ^ {\ infty} e ^ {- t ^ {2}} \, \ mathrm {d} t = {\ sqrt {\ pi}}}$

• Całki Fresnela

${\ displaystyle \ int _ {0} ^ {\ infty} \ cos t ^ {2} \, \ mathrm {d} t = \ int _ {0} ^ {\ infty} \ sin t ^ {2} \, \ mathrm {d} t = {\ tfrac {1} {4}} {\ sqrt {2 \ pi}}}$

• Całka Raabego

${\ displaystyle \ int \ limity _ {a} ^ {a + 1} \ log \ Gamma (t) \, \ mathrm {d} t = {\ tfrac {1} {2}} \ log 2 \ pi + a \ log aa, \ quad a \ geq 0,}$   a zwłaszcza dla i  :${\ styl wyświetlania a = 0}$${\ styl wyświetlania a = e}$${\ displaystyle \ int _ {0} ^ {1} \ log \ Gamma (t) \, \ mathrm {d} t = {\ tfrac {1} {2}} \ log 2 \ pi}$

• Całki Frullana

${\ displaystyle \ int _ {0} ^ {\ infty} {\ frac {f (ax) -f (bx)} {x}} \, \ mathrm {d} x}$

Integracja wielowymiarowa

Całki po ścieżce

Całki po trajektorii rzeczywistej i długość krzywej

Jeżeli istnieje ścieżki , to jest przekształcenie ciągłe i funkcji skalarnej, wówczas integralną ścieżki od wraz jest zdefiniowany jako ${\ displaystyle \ gamma \ dwukropek [a, b] \ do \ mathbb {R} ^ {n}}$${\ displaystyle f \ dwukropek \ mathbb {R} ^ {n} \ do \ mathbb {R}}$${\ styl wyświetlania f}$${\ styl wyświetlania \ gamma}$

${\ displaystyle \ int _ {\ gamma} f (x) \, \ mathrm {d} x = \ int _ {a} ^ {b} f (\ gamma (t)) \, \ | {\ kropka {\ gamma}} (t) \ | \, \ mathm {d} t.}$

Jeżeli , z powyższego wzoru otrzymujemy długość krzywej (fizycznie rzecz biorąc) jako całkę prędkości w czasie: ${\ displaystyle f \ ekwiwalent 1}$${\ displaystyle \ gamma \ dwukropek [a, b] \ do \ mathbb {R} ^ {2}}$

${\ displaystyle L (\ gamma) = \ int _ {a} ^ {b} \ | {\ kropka {\ gamma}} (t) \ | \, \ mathrm {d} t = \ int _ {a} ^ {b} {\ sqrt {{\ kropka {x}} (t) ^ {2} + {\ kropka {y}} (t) ^ {2}}} \, \ mathrm {d} t}$

Całki po ścieżce rzeczywistej dla funkcji wektorowych

W fizyce często stosuje się całki po trajektoriach postaci: jest funkcją wektorową i staje się całką ${\ displaystyle {\ vec {f}}}$${\ displaystyle \ mathbb {R} ^ {n} \ do \ mathbb {R} ^ {n}}$

${\ displaystyle \ int _ {\ gamma} {\ vec {f}} (x) \ cdot \ mathrm {d} x = \ int _ {a} ^ {b} \ langle {\ vec {f}} (\ gamma (t)), {\ kropka {\ gamma}} (t) \ rangle \, \ mathrm {d} t}$

rozważane, gdzie wyrażenie w nawiasach ostrych jest iloczynem skalarnym .

Całki złożone po ścieżce

W teorii funkcji , czyli poszerzeniu analizy o funkcje zmiennej zespolonej , nie wystarczy już określenie dolnej i górnej granicy całkowania. W przeciwieństwie do dwóch punktów na osi liczbowej, dwa punkty na płaszczyźnie zespolonej mogą być ze sobą połączone na wiele sposobów. Dlatego całka oznaczona w teorii funkcji jest w zasadzie całką po trajektorii . Twierdzenie resztkowe dotyczy zamkniętych ścieżek , ważny wynik Cauchy'ego: Całka funkcji meromorficznej wzdłuż ścieżki zamkniętej zależy wyłącznie od liczby zamkniętych osobliwości. Jest zero, jeśli nie ma osobliwości w obszarze integracji.

Całki powierzchniowe

Przykład: Obliczanie zawartości pomieszczenia

Jako przykład, objętość pomiędzy wykresem funkcji jest obliczana z na kwadrat jednostki . Aby to zrobić, dzieli się całkę na dwie całki, jedną dla - i jedną dla - współrzędnej: ${\ displaystyle f \ dwukropek \ mathbb {R} ^ {2} \ do \ mathbb {R}}$${\ displaystyle f (x, y): = x ^ {2} + y}$ ${\ styl wyświetlania I: = [0.1] \ razy [0.1]}$${\ styl wyświetlania I}$${\ styl wyświetlania x}$${\ styl wyświetlania y}$

${\ displaystyle {\ zacząć {wyrównany} \ int _ {[0,1] \ razy [0,1]} f (x, y) \, \ mathrm {d} (x, y) & = \ int _ { 0} ^ {1} \ int _ {0} ^ {1} f (x, y) \, \ mathrm {d} x \, \ mathrm {d} y = \ int _ {0} ^ {1} \ int _ {0} ^ {1} (x ^ {2} + y) \, \ mathrm {d} x \, \ mathrm {d} y \\ & = \ int _ {0} ^ {1} \ left [{\ tfrac {1} {3}} x ^ {3} + yx \ prawy] _ {x = 0} ^ {1} \, \ mathrm {d} y = \ int _ {0} ^ {1} \ lewo ({\ tfrac {1} {3}} + y \ prawy) \ mathrm {d} y = \ lewo [{\ tfrac {1} {3}} y + {\ tfrac {1} {2}} y ^ {2} \ prawy] _ {y = 0} ^ {1} = {\ tfrac {5} {6}} \ koniec {wyrównany}}}$

Dla całki powierzchniowej podaje się pole powierzchni całkowania. ${\ displaystyle f \ ekwiwalent 1}$

Całki z objętością

Dla całki z objętości oblicza zawartość objętości w obszarze całkowania. ${\ displaystyle f \ ekwiwalent 1}$

Integracja między obszarami wielowymiarowymi i wielowymiarowymi

Pojęcie całki można uogólnić w przypadku, gdy zbiorem nośników, na którym operuje całka, nie jest oś liczbowa , lecz dwuwymiarowa przestrzeń euklidesowa . ${\ styl wyświetlania f}$${\ styl wyświetlania \ mathbb {R}}$${\ styl wyświetlania n}$ ${\ styl wyświetlania \ mathbb {R} ^ {n}}$

Twierdzenie Fubiniego i twierdzenie o transformacji

W przypadku całek wielowymiarowych, czyli również całek powierzchniowych i objętościowych, stosuje się twierdzenie Fubiniego , które pozwala na rozdzielenie całek na poszczególne współrzędne w dowolnej kolejności i przetwarzanie jedna po drugiej:

${\ displaystyle {\ zacząć {wyrównany} \ int _ {V} f \ lewy ({\ vec {r}} \ prawy) \ mathrm {d} ^ {3} r & = \ iiint f (x, y, z ) \ mathrm {d} z \, \ mathrm {d} y \, \ mathrm {d} x \\ & = \ int \ left (\ int \ left (\ int f (x, y, z) \ mathrm { d } z \ po prawej) \ mathrm {d} y \ po prawej) \ mathrm {d} x \ end {wyrównane}}}$

Granice całkowania jednowymiarowych całek w , i muszą być określone na podstawie ograniczenia objętości . Analogicznie do całek niewłaściwych w jednowymiarze (patrz wyżej) można również rozważać całki po całej, nieograniczonej przestrzeni wymiarowej. ${\ styl wyświetlania x}$${\ styl wyświetlania y}$${\ styl wyświetlania z}$${\ styl wyświetlania V}$${\ styl wyświetlania n}$

Uogólnieniem zasady podstawienia w wielowymiarowym jest twierdzenie o przekształceniu . Bądź otwarty i injective , różniczkowalne w sposób ciągły odwzorowania, dla którego funkcjonalny wyznacznikiem dotyczy wszystkich . Następnie ${\ displaystyle \ Omega \ podzbiór \ mathbb {R} ^ {d}}$ ${\ displaystyle \ Phi \ dwukropek \ Omega \ do \ mathbb {R} ^ {d}}$ ${\ displaystyle \ det (D \ Phi (x)) \ neq 0}$${\ styl wyświetlania x \ w \ Omega}$

${\ displaystyle \ int _ {\ Phi (\ Omega)} f (y) \, \ mathrm {d} y = \ int _ {\ Omega} f (\ Phi (x)) \ lewo | \ det (D \ Phi (x)) \ prawo | \ mathrm {d} x.}$

Całki nad rozmaitościami

Integracja na powierzchni obszaru jest szczególnie interesująca w wielu zastosowaniach fizycznych. Takie powierzchnie są zwykle opisywane przez rozmaitości . Opisują je tzw. mapy.

Integracja na obszarze mapy

Pozwolić się wymiarową podrozmaitość i obszar mapy w , to jest podzbiorem otwartym w , na której znajduje się mapa , która mapuje go diffeomorphically na otwartym podzbiorze . Ponadto załóżmy parametryzację , tj. ciągle różniczkowalne odwzorowanie, którego wyprowadzenie ma pełną rangę, które odwzorowuje homeomorficznie na . Wtedy całka funkcji w obszarze mapy jest zdefiniowana w następujący sposób: ${\ styl wyświetlania M}$${\ styl wyświetlania d}$${\ styl wyświetlania \ mathbb {R} ^ {n}}$${\ styl wyświetlania U}$${\ styl wyświetlania M}$${\ styl wyświetlania M}$${\ displaystyle \ mathbb {R} ^ {d}}$${\ Displaystyle \ gamma \ dwukropek \ Omega \ do U}$${\ styl wyświetlania U}$${\ styl wyświetlania \ Omega}$ ${\ Displaystyle \ gamma (\ Omega)}$${\ styl wyświetlania U}$

${\ displaystyle \ int _ {U} f \ mathm {d} s: = \ int _ {\ Omega} f (\ gamma (u)) {\ sqrt {g ^ {\ gamma} (u)}} \ mathrm {d} ty,}$

gdzie jest tego wyznacznikiem Grama . Całkę właściwą można obliczyć za pomocą opisanych powyżej metod całkowania wielowymiarowego. Równość zasadniczo wynika z twierdzenia o transformacji. ${\ displaystyle g ^ {\ gamma} (u) = \ det ((\ gamma '(u)) ^ {\ mathsf {T}} \ cdot \ gamma' (u))}$

Integracja przez podrozmaitość

Jeśli istnieje podział 1, który jest zgodny z mapami podrozmaitości, można go po prostu zintegrować i dodać osobno na obszarach mapy.

Twierdzenie o całce Gaussa i twierdzenie Stokesa

W przypadku funkcji specjalnych całki można łatwiej obliczyć za pomocą podrozmaitości. W fizyce szczególnie ważne są dwa stwierdzenia:

Z jednej strony twierdzenie o całce Gaussa , zgodnie z którym całka objętościowa po rozbieżności pola wektorowego jest równa całce powierzchniowej po polu wektorowym ( przepływ pola przez powierzchnię): Bądź zwarty z gładką krawędzią w sekcjach . Niech krawędź będzie zorientowana przez zewnętrzne normalne pole jednostkowe . Ponadto, niech się różniczkowalne w sposób ciągły pole wektorowe na otwartym sąsiedztwie . Następnie dotyczy ${\ styl wyświetlania V \ podzbiór \ mathbb {R} ^ {n}}$ ${\ styl wyświetlania \ częściowy V}$${\ displaystyle {\ vec {n}}}$${\ displaystyle {\ vec {F}}}$${\ styl wyświetlania V}$

${\ displaystyle \ int _ {V} \ operatorname {div} {\ vec {F}} \, \ mathrm {d} ^ {(n)} V = \ oint _ {\ częściowy V} {\ vec {F} } \ cdot \ mathrm {d} ^ {(n-1)} {\ vec {S}}}$

ze skrótem . ${\ displaystyle \ mathrm {d} ^ {(n-1)} {\ vec {S}} = {\ vec {n}} \, \ mathrm {d} ^ {(n-1)} S}$

Zdanie to interpretuje dywergencję jako tzw. gęstość źródłową pola wektorowego. Wymiar odpowiedniego Równoległe dodatkowo podkreśla przez wskaźników lub przez operatora. ${\ styl wyświetlania (n)}$${\ styl wyświetlania (n-1)}$${\ styl wyświetlania \ matematyka {d}}$

Jeśli całki wielokrotne są używane jawnie (bez indeksowania) dla : ${\ styl wyświetlania n = 3}$

${\ displaystyle \ iiint _ {V} \ operatorname {div} \, {\ vec {F}} ({\ vec {x}}) \, \ mathrm {d} V = \ iint _ {\ częściowe V} { \ vec {F}} \ cdot \ mathrm {d} {\ vec {S}}}$

A więc: Całka dywergencji po całej objętości jest równa całce przepływu od powierzchni.

Po drugie, twierdzenie Stokesa , które jest stwierdzeniem geometrii różniczkowej iw szczególnym przypadku przestrzeni trójwymiarowej, może być zapisane bezpośrednio z całkami wielokrotnymi.

Jeśli istnieje dwuwymiarowa podrozmaitość trójwymiarowej przestrzeni euklidesowej , to ma zastosowanie ${\ styl wyświetlania M}$ ${\ styl wyświetlania \ mathbb {R} ^ {3}}$

${\ displaystyle \ iint _ {M} \ operatorname {rot} {\ vec {F}} \ cdot \ mathrm {d} {\ vec {S}} = \ int _ {\ częściowy M} {\ vec {F} } \ cdot \ mathrm {d} {\ vec {r}},}$

gdzie oznacza się obrót pola wektorowego . ${\ styl wyświetlania \ nazwa operatora {czerwony} {\ vec {F}}}$${\ displaystyle {\ vec {F}}}$

To zdanie interpretuje obrót pola wektorowego jako tzw. gęstość wirową pola wektorowego; gdzie wektor trójskładnikowy , a krawędź z zamkniętej krzywej im . ${\ displaystyle \ mathrm {d} {\ vec {r}}}$${\ styl wyświetlania (\ mathrm {d} x, \ mathrm {d} y, \ mathrm {d} z)}$${\ styl wyświetlania \ częściowy M}$${\ styl wyświetlania M}$${\ styl wyświetlania \ mathbb {R} ^ {3}}$

Całkowanie funkcji o wartościach wektorowych

Integracja funkcji, które nie są rzeczywiste ani o wartościach zespolonych, ale przyjmują wartości w bardziej ogólnej przestrzeni wektorowej, jest również możliwa na wiele różnych sposobów.

Bezpośrednim uogólnieniem całki Lebesgue'a na funkcje przestrzennie wartościujące Banacha jest całka Bochnera (za Salomonem Bochnerem ). Wiele wyników teorii jednowymiarowej przenosi się dosłownie na przestrzenie Banacha.

Przeniesienie definicji całki Riemanna do funkcji o wartościach wektorowych za pomocą sum Riemanna również nie jest trudne. Kluczowa różnica polega jednak na tym, że nie każda funkcja całkowalna Riemanna może być wtedy całkowalna Bochnera. ${\ displaystyle f \ dwukropek [a, b] \ do V}$

Powszechnym uogólnieniem całek Bochnera i Riemanna, które przezwycięża ten brak, jest całka McShane'a , którą najłatwiej zdefiniować za pomocą uogólnionych sum Riemanna.

Birkhoff integralną jest również częstym uogólnieniem całki Bochner i Riemanna. Jednak w przeciwieństwie do całki McShane'a, definicja całki Birkhoffa nie wymaga struktury topologicznej w obszarze definicji funkcji. Jeśli jednak spełnione są wymagania dotyczące integracji z McShane, każda funkcja integrowalna Birkhoffa może być również integrowalna z McShane.

Dodatkowo warto wspomnieć o całce Pettisa jako kolejnym kroku uogólniania. Wykorzystuje funkcjonalny analitycznej definicji, w którym Całkowalność sprowadza się do jednowymiarowego przypadku: Niech będzie przestrzeń miarą . Funkcja nazywa się całkowalną Pettisa, jeśli funkcja całkowalna Lebesgue'a dla każdego funkcjonału ciągłego i wektor istnieje dla każdego zbioru mierzalnego , tak że ${\ styl wyświetlania (\ Omega, {\ mathcal {A}}, \ mu)}$${\ displaystyle f \ dwukropek \ Omega \ do V}$${\ displaystyle \ lambda \ w V '}$${\ displaystyle \ lambda \ circ f \ dwukropek \ Omega \ do \ mathbb {R}}$${\ styl wyświetlania A \ w {\ mathcal {A}}}$${\ styl wyświetlania x_ {A} \ w V}$

${\ displaystyle \ forall \ lambda \ in V '\ dwukropek \ \ lambda (x_ {A}) = \ int _ {A} {\ lambda \ circ f} \, \ mathrm {d} \ mu}$

ma zastosowanie. Wektor zostaje następnie odpowiednio nazwany z . ${\ styl wyświetlania x_ {A}}$${\ displaystyle \ textstyle \ int _ {A} f \, \ mathrm {d} \ mu}$

Dla funkcji, które przyjmują wartości w separowalnej przestrzeni Banacha , całka Pettisa zgadza się z całkami McShane'a i Bochnera. Najważniejszym szczególnym przypadkiem wszystkich tych definicji jest przypadek funkcji w , które są po prostu zintegrowane składnik po składniku we wszystkich tych definicjach. ${\ displaystyle f \ dwukropek [a, b] \ do V}$${\ styl wyświetlania V}$${\ styl wyświetlania \ mathbb {R} ^ {n}}$

Uogólnienia

Pojęcie całka zostało rozwinięte na wiele sposobów, niektóre warianty to:

• Całka Riemanna
• Całka Daniella
• Całka Stieltjesa
• Całka Itō i Całka Stratonowitscha , patrz także Całka stochastyczna dyskretna
• Całka Gauge lub całka Henstocka-Kurzweila , a w szczególności:
  • Całka McShanea
  • Całka pieprzowa
• Zmierz całkę
  • Całka Lebesgue'a
  • Całka Bochnera
  • Całka Birkhoffa
  • Całka Pettisa
  • Włosy integralne
• Całka Volkenborna

Teoria miary

Owłosiona miara

Miara Haara, po Alfréd Haar , reprezentuje uogólnienie miary Lebesgue'a dla lokalnie zwartych grup topologicznych, a zatem również indukuje całkę jako uogólnienie całki Lebesgue'a.

Całkowanie na rozmaitościach

Zobacz: Integracja form różniczkowych

Wreszcie integracja może być również wykorzystana do pomiaru powierzchni danych ciał. Prowadzi to do dziedziny geometrii różniczkowej .

Zobacz też

• Całkowanie algebraiczne
• Integracja stochastyczna
• Tabela funkcji pochodnych i funkcji pierwotna
• Całka Volkenborna

literatura

• Książki szkolne:
  • Rachunek całkowy jest głównym przedmiotem na poziomie szkoły średniej II stopnia i dlatego jest omawiany we wszystkich podręcznikach do matematyki.
• Podręczniki dla studentów matematyki i przedmiotów pokrewnych (fizyka, informatyka):
  • Herbert Amann, Joachim Escher : Analiza I, II, III. Birkhäuser-Verlag Basel Boston Berlin, ISBN 3-7643-7755-0 , ISBN 3-7643-7105-6 , ISBN 3-7643-6613-3 .
  • Richard Courant : Wykłady z rachunku różniczkowego i całkowego 1, 2. Springer, 1. wydanie 1928, 4. wydanie 1971.
  • Gregor Michailowitsch Fichtenholz : Rachunek różniczkowy i całkowy I – III. Wydawnictwo Harri Deutsch, Frankfurt nad Menem, 1990–2004. ISBN 978-3-8171-1418-4 (kompletny zestaw).
  • Otto Forster : Analiza 1. Rachunek różniczkowy i całkowy zmiennej. Wydanie 7. Vieweg-Verlag, 2004. ISBN 3-528-67224-2 .
  • Otto Forster: Analiza. Tom 3: Teoria miary i całkowania, twierdzenia całkowe w R ⁿ i zastosowaniach , wydanie 8 poprawione. Springer Spectrum, Wiesbaden, 2017, ISBN 978-3-658-16745-5 .
  • Konrad Königsberger : Analiza. 2 tomy, Springer, Berlin 2004.
  • Vladimir Ivanovich Smirnov : Kurs matematyki wyższej (części 1-5). Wydawnictwo Harri Deutsch, Frankfurt nad Menem, 1995–2004. ISBN 978-3-8171-1419-1 (kompletny zestaw).
  • Steffen Timmann: Repetitorium der Analysis 1, 2. 1. wydanie. Binomi Verlag, 1993.
• Podręczniki dla uczniów z przedmiotu drugorzędnego/podstawowego z matematyki (np. dla studentów inżynierii lub ekonomii):
  • Rainer Ansorge i Hans Joachim Oberle: Matematyka dla inżynierów. Tom 1. Wydanie trzecie. Wiley-VCH, 2000.
  • Lothar Papula : Matematyka dla przyrodników i inżynierów. Tom 1. Wydanie 13. Zobacz + Teubner Verlag. ISBN 978-3-8348-1749-5 .
• Historyczny:
  • Adolph Mayer: Przyczynki do teorii maksimów i minimów całek prostych. Teubner, Lipsk 1866 ( wersja zdigitalizowana ).
  • Bernhard Riemann: O przedstawialności funkcji przez szereg trygonometryczny. Göttingen 1867 ( pełny tekst ), z pierwszą definicją całki Riemanna (str. 12 ff.).

linki internetowe

• Kalkulator online do obliczania całek (pierwotnych) z metodą obliczania i objaśnieniami (niemiecki)
• mathe-online.at - Zasoby na temat integracji (poziom II stopnia / FHS / Uni)
• Jasne wyjaśnienia
• The Integrator - strona w języku angielskim do obliczania całek
• Kalkulator całkowy - niemiecka strona do obliczania całek oznaczonych i nieoznaczonych (pierwiastki)
• Część 1 trzyczęściowej serii całek wielokrotnych (szczegółowe + obszerne)
• 50 przykładów funkcji korzenia przykłady funkcji
• Wideo: całka, pierwotna . Jörn Loviscach 2010, udostępniony przez Bibliotekę Informacji Technicznych (TIB), doi : 10.5446 / 9752 .
• Wideo: pochodna, całka, przypadek . Jörn Loviscach 2010, udostępniony przez Bibliotekę Informacji Technicznych (TIB), doi : 10.5446 / 9736 .
• Wideo: całka oznaczona 1 . Jörn Loviscach 2010, udostępniony przez Bibliotekę Informacji Technicznych (TIB), doi : 10.5446 / 9755 .
• Wideo: całka oznaczona 2 . Jörn Loviscach 2010, udostępniony przez Bibliotekę Informacji Technicznych (TIB), doi : 10.5446 / 9756 .

Indywidualne dowody

1. ↑ D. Fremlin: Całki McShane'a i Birkhoffa funkcji o wartościach wektorowych. ( Pamiątka z 28 kwietnia 2015 r. w Internetowym Archiwum ).